Tři množiny
Až doposud jsme si ukázali práci s Vennovými diagramy i s množinovými operacemi pouze pro dvě množiny. Ovšem v praxi se setkáváme i s podstatně většími počty množin. I na nich můžeme postupně provádět množinové operace (tak jako můžeme např. postupně sečíst tři čísla) a také pro ně můžeme použít Vennovy diagramy. Vennův diagram – jak jsme si již řekli – lze vytvořit pro libovolný konečný počet množin, my si však v této práci většinou vystačíme s diagramem pro dvě nebo pro tři množiny:
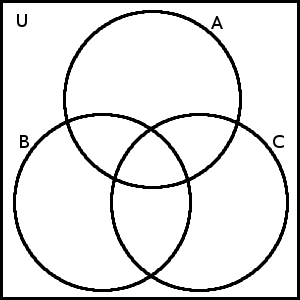
Vennův diagram pro tři množiny \(A\), \(B\) a \(C\)
Tento diagram je opět univerzální a opět jej využijeme k ověřování různých pravidel pro práci s množinami. Zkusme například zjistit, zda je operace průniku asociativní, tedy zda platí (\(A \cap B\)) \(\cap\) \(C\) = \(A\) \(\cap\) (\(B \cap C\)).
Zakreslíme nejdříve levou stranu, tj. začneme množinou \(A \cap B\):
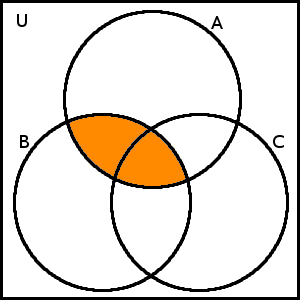
\(A \cap B\)
Co bude výsledným průnikem je asi zřejmé, přesto si však ještě vyšrafujme množinu \(C\):
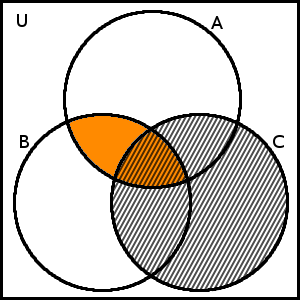
\(A \cap B\) a množina \(C\)
Výsledným průnikem je množina, která je na obrázku výše podbarvena i vyšrafována:
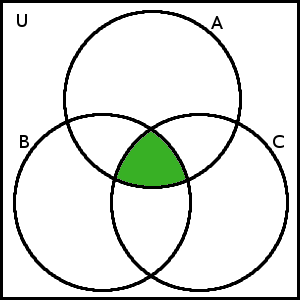
(\(A \cap B\)) \(\cap\) \(C\)
Nyní se podívejme na pravou stranu rovnosti. Nejprve zakreslíme množinu \(B \cap C\):

\(B \cap C\)
Vyšrafujme ještě množinu \(A\):
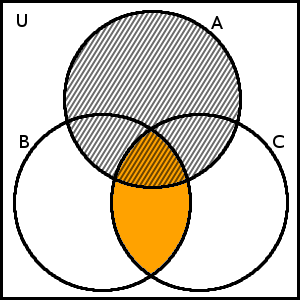
\(B \cap C\) a množina \(A\)
Výsledným průnikem je opět množina, která je na obrázku výše podbarvená oranžovou barvou a zároveň vyšrafovaná:

\(A\) \(\cap\) (\(B \cap C\))
Pro levou i pravou stranu jsme získali stejný diagram, rovnost tedy platí. Z toho plyne, že operace průniku je asociativní. Pokud budeme postupně provádět několik průniků, nemusíme tedy používat závorky, místo (\(A \cap B\)) \(\cap\) \(C\) můžeme rovnou psát \(A \cap B\) \(\cap\) \(C\).
Toto platí i pro sjednocení, tj. operace sjednocení je asociativní. Ověření tohoto pravidla zde provádět nebudeme, avšak je to vhodná příležitost k procvičení.
Již při zavádění operací sjednocení a průniku jsme si ukázali, že tyto operace jsou komutativní. Nyní víme, že jsou také asociativní, a tak můžeme zapsat např. následující rovnosti platící pro libovolnou trojici množin:
\(A \cap B\) \(\cap\) \(C\) = \(A \cap C\) \(\cap\) \(B\) = \(B \cap A\) \(\cap\) \(C\) = \(B \cap C\) \(\cap\) \(A\) = \(C \cap B\) \(\cap\) \(A\) = \(C \cap A\) \(\cap\) \(B\)
\(A\cup B\) \(\cup\) \(C\) = \(A\cup C\) \(\cup\) \(B\) = \(B\cup A\) \(\cup\) \(C\) = \(B\cup C\) \(\cap\) \(A\) = \(C\cup B\) \(\cap\) \(A\) = \(C\cup A\) \(\cap\) \(B\)
Podobné rovnosti bychom mohli psát také pro čtveřice množin, pětice,… Zkrátka s průnikem a sjednocením konečného počtu množin můžeme zacházet podobně jako se sčítáním a násobením u čísel. U čísel však platí také tzv. distributivní zákon – platí jeho obdoba i u množin? Zkusme to odvodit s využitím Vennových diagramů.
Máme ověřit, že platí \(A\) \(\cap\) (\(B\cup C\)) = (\(A \cap B\)) \(\cup\) (\(A \cap C\)), neboli že platí distributivnost průniku vůči sjednocení. Začneme nejdříve levou stranou rovnosti, zakreslíme nejprve množinu \(B\cup C\) a množinu \(A\), potom zachytíme jejich průnik:
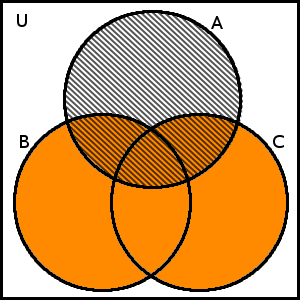
\(B\cup C\) a množina \(A\)
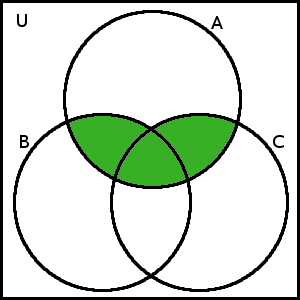
\(A\) \(\cap\) (\(B\cup C\))
Zbývá znázornit pravou stranu rovnosti, tj. nejdříve množiny \(A \cap B\) a \(A \cap C\) a potom jejich sjednocení:
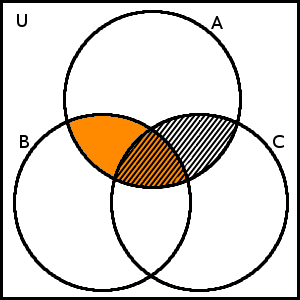
\(A \cap B\) a množina \(A \cap C\)

(\(A \cap B\)) \(\cup\) (\(A \cap C\))
Vybarvené oblasti ve výsledných diagramech jsou opět shodné, rovnost \(A\) \(\cap\) (\(B\cup C\)) = (\(A \cap B\)) \(\cup\) (\(A \cap C\)) platí pro libovolné tři množiny \(A\), \(B\) a \(C\).
Tento vztah platí i v případě, že zaměníme průniky a sjednocení, tj. budeme-li uvažovat rovnost \(A\) \(\cup\) (\(B \cap C\)) = (\(A\cup B\)) \(\cap\) (\(A\cup C\)). Postup ověření je podobný jako v předchozím případě, proto si je nebudeme znovu ukazovat. Je to však dobré cvičení!
I u těchto vztahů o „distributivitě“ množinových operací můžeme uvažovat o variantě pro výroky (podobně jako jsme to učinili u De Morganových vzorců). Pokud zaměníme množiny za výroky, průnik za konjunkci, sjednocení za disjunkci a rovnost za ekvivalenci, získáme tautologie. Ověření lze provést např. tabulkou pravdivostních hodnot. Ukažme si tabulku pro případ [\(\mathbf{A}\) \(\wedge\) (\(\mathrm{\mathbf{B}}\vee \mathrm{\mathbf{C}}\))] \(\Leftrightarrow\) [(\(\mathbf{A} \wedge \mathbf{B}\)) \(\vee\) (\(\mathbf{A} \wedge \mathbf{C}\))]:
| A | B | C | \(\mathrm{\mathbf{B}}\vee \mathrm{\mathbf{C}}\) | \(\mathbf{A}\) \(\wedge\) (\(\mathrm{\mathbf{B}}\vee \mathrm{\mathbf{C}}\)) | \(\mathbf{A} \wedge \mathbf{B}\) | \(\mathbf{A} \wedge \mathbf{C}\) | (\(\mathbf{A} \wedge \mathbf{B}\)) \(\vee\) (\(\mathbf{A} \wedge \mathbf{C}\)) | \(\mathbf{A}\) \(\wedge\) (\(\mathrm{\mathbf{B}}\vee \mathrm{\mathbf{C}}\)) \(\Leftrightarrow\) (\(\mathbf{A} \wedge \mathbf{B}\)) \(\vee\) (\(\mathbf{A} \wedge \mathbf{C}\)) |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Druhý případ, tj. [\(\mathbf{A}\) \(\vee\) (\(\mathbf{B} \wedge \mathbf{C}\))] \(\Leftrightarrow\) [(\(\mathrm{\mathbf{A}}\vee \mathrm{\mathbf{B}}\)) \(\wedge\) (\(\mathrm{\mathbf{A}}\vee \mathrm{\mathbf{C}}\))], si už ukazovat nebudeme, necháme ho opět k samostatnému procvičení.
V této části jsme si ukázali, že Vennových diagramů můžeme použít nejen pro grafické znázornění situací mezi množinami, ale také pro ověřování různých vztahů a obecně platných pravidel. Vennovy diagramy však mohou sloužit i pro řešení konkrétních příkladů a také ke zjednodušování složitějších množinových zápisů.
