Shrnutí
| Vztah nebo operace | Značení | Symbolické vyjádření | Vennův diagram |
|---|---|---|---|
| Podmnožina množiny | \(B \subseteq A\) | \(B \subseteq A\) \(\Leftrightarrow\) [\(\forall (x \in U)\): \(\mathrm{x\in B}\Rightarrow \mathrm{x\in A}\)] | 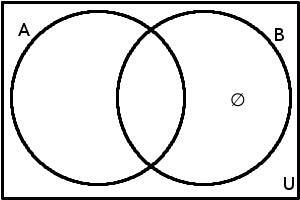 |
| Rovnost množin | \(A\) = \(B\) | \(A\) = \(B\) \(\Leftrightarrow\) [\(B \subseteq A\) \(\wedge\) \(A \subseteq B\)] | 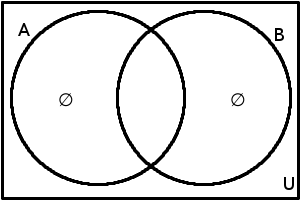 |
| Průnik množin | \(A \cap B\) | \(A \cap B\) = {\(x\)\(\in\)\(U\); \(x\in A \wedge x\in B\)} | 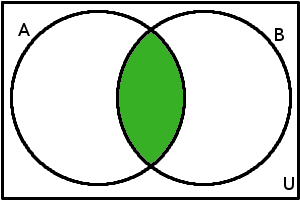 |
| Sjednocení množin | \(A\cup B\) | \(A\cup B\) = {\(x\)\(\in\)\(U\); \(\mathrm{x\in A}\vee \mathrm{x\in B}\)} | 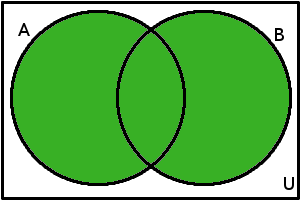 |
| Rozdíl množin | \(A \setminus B\) | \(A \setminus B\) = {\(x\)\(\in\)\(U\); \(x\in A \wedge x\notin B\)} | 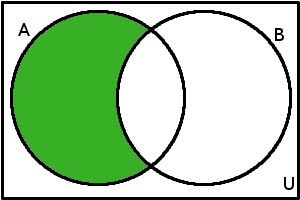 |
| Doplněk množiny (vzhledem k základní množině \(U\)) |
\(A'\) | \(A'\) = {\(x\)\(\in\)\(U\); \(x\)\(\notin\)\(A\)} | 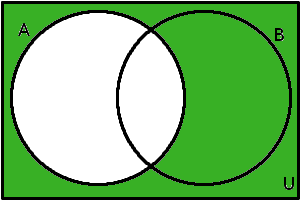 |
