Doplněk množiny
Mějme dvě množiny \(A\) a \(B\), kde navíc platí \(B\) \(\subseteq\) \(A\). V takové situaci zavádíme pojem doplněk množiny.
Je-li \(B\) \(\subseteq\) \(A\), pak doplňkem množiny \(B\) vzhledem k množině \(A\) je množina, která obsahuje všechny prvky z \(A\), které zároveň nejsou v \(B\).
Doplněk množiny \(B\) vzhledem k množině \(A\) budeme značit \(B'\)\(_A\). Pokud je z předchozího kontextu jasné, k jaké množině je doplněk vztažen, můžeme psát zkráceně \(B\)'. Je asi také zřejmé, že operace doplňku není komutativní, neboli když zaměníme pozice množin \(A\) a \(B\), nedostaneme stejný výsledek (nejen to, dokonce pak většinou není možné o doplňku mluvit, protože je porušena podmínka inkluze). Graficky si můžeme doplněk znázornit následovně (doplněk je vyznačen šrafováním):
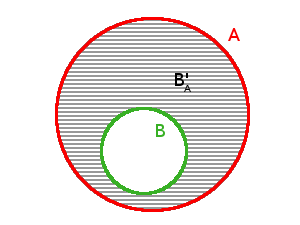
\(B'\)\(_A\)
Řekli jsme si, že doplněk je také množina, zavedli jsme si tedy operaci, která nám umožňuje definovat novou množinu ze dvou již známých množin. Nesmíme však zapomenout na podmínku, že množina, jejíž určujeme doplněk, musí být podmnožinou množiny, vzhledem ke které se doplněk tvoří! Nyní si ukažme několik příkladů na konkrétních množinách:
- Budeme-li za \(A\) považovat množinu všech trojúhelníků v nějaké dané rovině a množina \(B\) bude množina všech ostroúhlých trojúhelníků tamtéž, pak množina \(B'\)\(_A\) bude množina všech tupoúhlých a pravoúhlých trojúhelníků v dané rovině – z množiny \(A\) totiž odebereme všechny prvky obsažené zároveň v její podmnožině \(B\) (tedy všechny ostroúhlé trojúhelníky).
- Mějme množiny \(A\) = {1, 2, 3, 4, 5, 6} a \(B\) = {1, 3, 6}. Pak je množina \(B'\)\(_A\) = {2, 4, 5}.
- Jsou dány množiny \(C\) = {\(x \)\(\in\) \(\mathbb{N}\); \(x\) > 5} a \(D\) = {6, 7}. Pak je množina \(D'\)\(_C\) = {\(x \)\(\in\) \(\mathbb{N}\); \(x\) > 7}.
- Říkali jsme si, že množina je sama sobě podmnožinou. Máme-li množinu \(M\), pak \(M'\)\(_M\) = \(\emptyset\).
Pokud použijeme obrazné vyjadřování, můžeme říci, že doplněk množiny \(B\) vzhledem k množině \(A\) je právě ten „zbytek“ množiny \(A\), který zbyde po „odstřižení“ její podmnožiny \(B\).
