Průnik množin
Poslední operací, kterou si ukážeme, je průnik množin. Tato operace nám umožňuje ukázat, co mají množiny společné. Budeme ji značit symbolem, který připomíná horizontálně převrácený symbol pro sjednocení, tj. „\(\cap\)“.
Průnik množin \(A\) a \(B\), který značíme \(A \cap B\), je množina všech prvků, které jsou obsaženy v množině \(A\) a současně i v množině \(B\).
Průnikem dvou množin získáme množinu, která obsahuje jen ty prvky, které jsou pro dané dvě množiny společné. V grafickém znázornění zohledníme to, že společné prvky mají být naznačeny překrytím kruhů, jež symbolizují množiny:
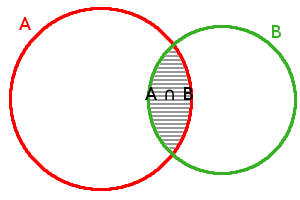
\(A \cap B\)
Jestliže dvě množiny nemají žádné společné prvky, neboli jejich průnikem je prázdná množina, pak o těchto množinách říkáme, že jsou disjunktní. Je to velmi důležitá vlastnost dvojice množin, protože je z ní možné odvodit mnoho dalších poznatků. Platí například, že mohutnost sjednocení dvou disjunktních konečných množin je součtem mohutností sjednocovaných množin. Chceme-li naznačit opačnou situaci – tedy že množiny mají nějaké společné prvky – používáme často spojení, že množiny mají neprázdný průnik.
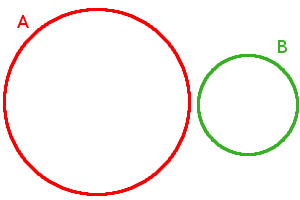
Disjunktní množiny
K dobrému pochopení operace průniku si opět ještě můžeme pomoci ukázkou několika příkladů:
- Uvažujme nějakou kuchyňskou skříňku s nádobím. Řekněme, že množina \(A\) je množina všech hrnečků ve skříňce, množinou \(B\) je pak množina všeho skleněného nádobí ve skříňce. Množina \(A \cap B\) je pak množina všech skleněných hrnečků ve skříňce. Pokud v ní žádné skleněné hrnečky nejsou, jsou množiny \(A\) a \(B\) disjunktní.
- Mějme množiny \(A\) = {1, 2, 3, 4, 5, 6} a \(B\) = {3, 6, 8, 9}. Pak \(A \cap B\) = {3, 6}.
- \(A\) = {−1, 2, 3, 4, 5, 6} a \(B\) = \(\mathbb{Q}\). Pak \(A \cap B\) = {−1, 2, 3, 4, 5, 6} = \(A\).
- Mějme množiny \(A\) = {1, 2, 3, 6} a \(B\) = \(\emptyset\). Pak \(A \cap B\) = \(\emptyset\). Prázdná množina totiž neobsahuje vůbec žádné prvky, a tak nemůže mít s jinou množinou nějaký společný prvek.
- Předchozí příklad lze zobecnit na průnik libovolné množiny a prázdné množiny. Ten je totiž v takovém případě vždy prázdný. Neboli, pro libovolnou množinu \(A\) platí: \(A \cap \emptyset\) = \(\emptyset\).
- Podobně se můžeme zamyslet nad tím, jak je to s průnikem množiny a její podmnožiny. Tím bude právě ona podmnožina – tedy: Je-li \(A \subseteq B\), pak \(A \cap B\) = \(A\).
- Průnikem libovolné množiny se sebou samou je opět sama tato množina, množiny zúčastněné v tomto průniku mají společné právě všechny prvky: \(M \cap M\) = \(M\).
Je zřejmé, že tato operace je komutativní. Vybíráme totiž prvky společné pro obě množiny a je lhostejné, u které začneme. Pro libovolné dvě množiny \(A\) a \(B\) platí: \(A \cap B\) = \(B \cap A\).
