De Morganovy vzorce
Tyto vzorce jsou pojmenovány po britském matematikovi Augustu De Morganovi, jenž v 19. století zformuloval mnoho logických pravidel a zákonů. Ukažme si, jak vypadají tyto vzorce pro dvě množiny:
- (\(A\cup B\))' = \(A' \cap B'\)
- (\(A \cap B\))' = \(A'\cup B'\)
Platí tyto vzorce opravdu pro všechny množiny? Tomu sice můžeme věřit, ale nejlepší je si to ověřit. Zkusme k tomu využít Vennovy diagramy. Ty nám totiž umožňují pracovat s množinami obecně. Začneme s prvním vzorcem, zakreslíme do diagramu nejdříve jeho levou a poté i pravou stranu. Levá strana prvního vzorce je doplněk sjednocení množin. Nejdříve tedy zakreslíme sjednocení množin a potom provedeme jeho doplněk:
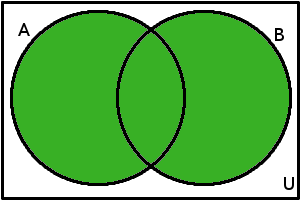
\(A\cup B\)
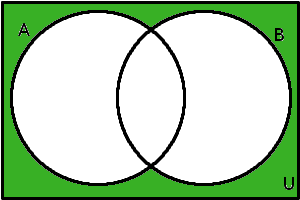
(\(A\cup B\))'
Teď už víme, jaká množina se skrývá pod zápisem na levé straně rovnosti v prvním vzorci. Nyní se podívejme na jeho pravou stranu, tj. na množinu \(A' \cap B'\). Je to průnik doplňků, musíme tedy nejdříve najít doplňky a pak provést jejich průnik. V následujícím diagramu je žlutě označen doplněk množiny \(A\), šrafováním je vyznačen doplněk množiny \(B\).
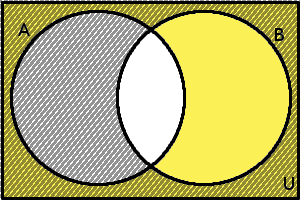
Množiny \(A'\) a \(B'\)
Co je průnikem těchto dvou doplňků je zřejmé – je to ta část diagramu, která je podbarvena žlutě a zároveň je šrafovaná. Označme tuto část zeleně a podívejme se, zda se shoduje s tím, co jsme si namalovali výše u množiny (\(A\cup B\))':

\(A' \cap B'\)
Diagramy jsou stejné, rovnost (\(A\cup B\))' = \(A' \cap B'\) platí. Bez Vennových diagramů bychom tento vztah obecně dokazovali složitěji. Zkusme ještě ověřit platnost druhého vzorce, tj. (\(A \cap B\))' = \(A'\cup B'\). Levá strana rovnosti je tentokrát doplňkem průniku – zakreslíme nejdříve průnik a poté jeho doplněk:
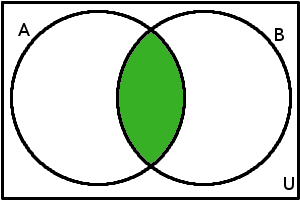
\(A \cap B\)
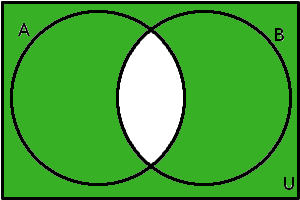
(\(A \cap B\))'
Levá strana je znázorněna, podívejme se na tu pravou. Pravá strana je sjednocením doplňků. Doplňky množin \(A\) a \(B\) jsme si již do diagramu zakreslili při ověřování předchozího vztahu:

Množiny \(A'\) a \(B'\)
Po jejich sjednocení zůstane v diagramu bílé pouze to, co nebylo obsaženo ani v jednom z těchto doplňků. Vlastní sjednocení doplňků opět vyznačíme zeleně:

\(A'\cup B'\)
Porovnáme-li oba diagramy, zjistíme opět, že ověřovaný vztah platí (diagramy jsou shodné).
V tuto chvíli bychom už měli nejen vědět, že De Morganovy vztahy platí pro libovolné množiny (při našem ověřování jsme si množiny \(A\) a \(B\) nijak blíže nespecifikovali), ale také bychom měli mít přibližnou představu, co vlastně např. zápis (\(A \cap B\))' představuje.
De Morganovy vzorce však nemusíme aplikovat pouze na množiny. Vzpomeňme si na výroky. Zkusme množinu nahradit výrokem, doplněk negací, průnik konjunkcí, sjednocení disjunkcí a rovnost ekvivalencí:
- [¬(\(\mathrm{\mathbf{A}}\vee \mathrm{\mathbf{B}}\))] \(\Leftrightarrow\) (\(¬\mathbf{A} \wedge ¬\mathbf{B}\))
- [¬(\(\mathbf{A} \wedge \mathbf{B}\))] \(\Leftrightarrow\) (\(\mathrm{¬\mathbf{A}}\vee \mathrm{¬\mathbf{B}}\))
Jsou tyto ekvivalence tautologiemi (jsou vždy pravdivé)? Samozřejmě, jde o zápis negace konjunkce a disjunkce. Právě v takové podobě jsme si tyto negace v kapitole o logických spojkách odvodili.
Jak již bylo řečeno v úvodu, tyto de Morganovy vzorce můžeme ověřit i jiným způsobem. Ukažme si nyní na prvním z nich – (\(A\cup B\))' = \(A' \cap B'\) – jak lze v takovém případě postupovat. Nejprve ukážeme, že platí (\(A\cup B\))' \(\subseteq\) \(A' \cap B'\), a poté ověříme i obrácenou inkluzi \(A' \cap B'\) \(\subseteq\) (\(A\cup B\))', čímž prokážeme, že platí rovnost.
Náleží-li nějaký libovolný prvek \(x\) do množiny (\(A\cup B\))', tj. \(x \)\(\in\) (\(A\cup B\))', pak z definice doplňku plyne, že \(x \)\(\notin\) (\(A\cup B\)). Žádný prvek totiž nemůže náležet nějaké množině a zároveň i jejímu doplňku. Jestliže ale \(x \)\(\notin\) (\(A\cup B\)), pak \(x\) nemůže být prvkem ani množiny \(A\) ani množiny \(B\), tj. (\(x\) \(\notin\) \(A\)) \(\wedge\) (\(x\) \(\notin\) \(B\)). Když prvek nějaké množině nenáleží, musí náležet jejímu doplňku. Z toho plyne, že (\(x\) \(\in\) \(A'\)) \(\wedge\) (\(x\) \(\in\) \(B'\)). Tento zápis však můžeme přepsat pomocí průniku \(x \)\(\in\) (\(A' \cap B'\)). Je-li totiž \(x\) prvkem obou množin, musí být i prvkem jejich průniku. Ukázali jsme, že zvolíme-li jakýkoli prvek z množiny (\(A\cup B\))', musí tento prvek ležet i v množině \(A' \cap B'\). Tím jsme ověřili první inkluzi (\(A\cup B\))' \(\subseteq\) \(A' \cap B'\).
Pro ověření obrácené inkluze stačí v tomto případě pouze otočit postup z předchozího odstavce. Jestliže je \(x\) prvkem průniku doplňků množin \(A\) a \(B\), tj. \(x \)\(\in\) (\(A' \cap B'\)), pak musí být také prvkem množin \(A'\) i \(B'\), atd. Platí-li obě inkluze, musí platit i rovnost.
Vidíme, že platnost uvedného vztahu lze prokázat i metodami, které Vennových diagramů nevyužívají. Každá z těchto metod má své výhody, největší výhodou Vennových diagramů je grafická ilustrace vztahů mezi množinami.
Zkusme si nyní pomocí Vennových diagramů ověřit ještě jiný vztah, který platí pro libovolnou dvojici množin: \(A \setminus B\) = \(A \cap B'\). Levou stranu umíme znázornit hned:
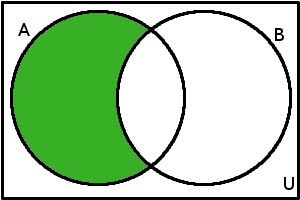
\(A \setminus B\)
Pro zkonstruování obrazu množiny na pravé straně rovnosti musíme nejdříve najít doplněk množiny \(B\):
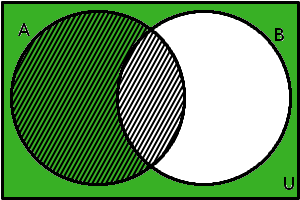
\(B'\) a \(A\)
Doplněk množiny \(B\) je vyznačen zeleně, množina \(A\) je vyšrafována. Průnikem je tedy množina, která je v diagramu zelená a zároveň vyšrafovaná:

\(A \cap B'\)
Diagram pro levou a pravou stranu rovnosti se opět shoduje, rovnost skutečně platí. Podobně jako jsme u výroků zjistili, že jednotlivé logické spojky je možné nahradit kombinací jiných, vidíme totéž i u množinových operací. Tento poslední příklad ukazuje právě způsob, jak zapsat rozdíl pomocí průniku a doplňku.
