Množinové operace ve Vennových diagramech
Do Vennova diagramu můžeme také snadno zaznamenat množinové operace, které jsme si výše ukázali. Začněme například průnikem. V následujícím diagramu je zelenou barvou vyznačena množina, která je průnikem množin \(A\) a \(B\).
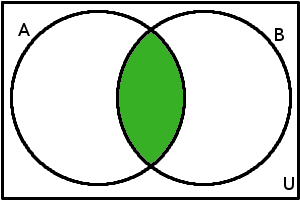
\(A \cap B\) = {\(x\)\(\in\)\(U\); \(x\in A \wedge x\in B\)}
Operace sjednocení a rozdílu následují na dalších obrázcích:
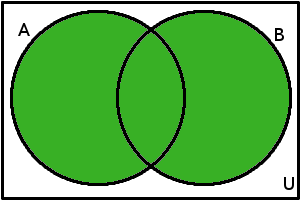
\(A\cup B\) = {\(x\)\(\in\)\(U\); \(\mathrm{x\in A}\vee \mathrm{x\in B}\)}
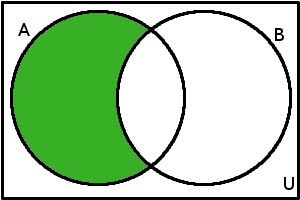
\(A \setminus B\) = {\(x\)\(\in\)\(U\); \(x\in A \wedge x\notin B\)}
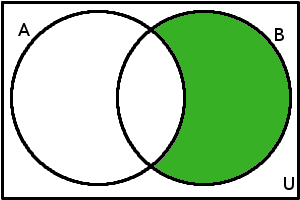
\(B \setminus A\) = {\(x\)\(\in\)\(U\); \(x\notin A \wedge x\in B\)}
Chybí ještě doplněk. Mohli bychom si ukázat doplněk množiny \(B\) vzhledem k \(A\) (resp. množiny \(A\) vzhledem k \(B\)), samozřejmě za patřičného předpokladu \(B \subseteq A\) (resp. \(A \subseteq B\)). Diagramy pro tyto situace by vypadaly stejně jako diagramy zachycující rozdíl množin (vzpomeňme si, že platí-li \(B \subseteq A\), pak \(A \setminus B\) = \(B\)'\(_A\)).
Máme-li však zvolenou základní množinu, často se provádí doplněk vzhledem k této základní množině. V takové situaci obvykle nezapisujeme, že doplněk děláme vzhledem k základní množině, ale např. doplněk množiny \(A\) značíme \(A\)'.
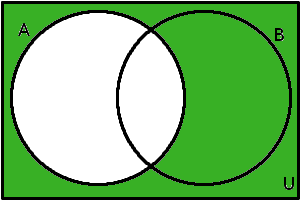
\(A'\) = {\(x\)\(\in\)\(U\); \(x\)\(\notin\)\(A\)}
Grafické znázornění množinových operací vypadá ve Vennových diagramech podobně jako na obrázcích, které jsme si ukazovali přímo u zavádění těchto operací. Zatím jsme si tedy v podstatě neukázali, v čem tkví hlavní výhody Vennových diagramů. Jejich univerzálnost, která nám pomůže si uvědomit, jaké situace mohou mezi množinami nastat, se však brzy projeví, začneme-li provádět složitější operace.
Zatím jsme s množinami prováděli pouze jednoduché operace. Zkusme je nyní zkombinovat. Abychom však nemuseli psát velká množství závorek, dohodněme se, jakou budou mít jednotlivé operace prioritu (stejně jako u čísel víme, že násobení má přednost před sčítáním). Uvažujme např. množinu \(A\cup B'\). V tuto chvíli neumíme říci, zda tento zápis znamená sjednocení množiny \(A\) s doplňkem množiny \(B\) anebo zda se jedná o doplněk sjednocení množin \(A\) a \(B\). Dohodněme se, že doplněk má vyšší prioritu než ostatní operace. Uvedený zápis tedy znamená sjednocení množiny \(A\) s doplňkem množiny \(B\), druhou zmiňovanou variantu bychom zapsali s pomocí závorek takto: (\(A\cup B\))'.
Uvažujme tedy množinu \(A\cup B'\) za předpokladu, že základní množina \(U\) = \(\mathbb{N}\), \(A\) = {4, 5, 6, 7, 8} a \(B\) = {1, 2, 3, 4}. Nyní zkusme s pomocí Vennova diagramu vyřešit, jak vlastně množina \(A\cup B'\) vypadá. Postup bude podobný, jako když jsme vyšetřovali pravdivostní ohodnocení složených výroků. Půjdeme postupně, dokud nezískáme informaci o celé vyšetřované množině. V našem příkladu začneme doplňkem množiny \(B\). Ten potřebujeme znát, abychom jej mohli sjednotit s množinou \(A\). Dokud nevíme, jak tento doplněk vypadá, nemůžeme sjednocení provádět. Zakresleme tedy do Vennova diagramu množinu \(B'\):
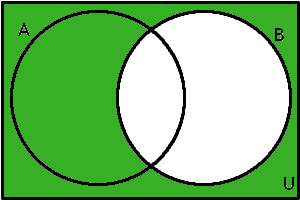
\(B'\)
Nyní do diagramu zachytíme sjednocení s množinou \(A\). K tomu stačí pouhé vyšrafování množiny \(A\) (druhou sjednocovanou množinu jsme vybarvili v předchozím kroku):
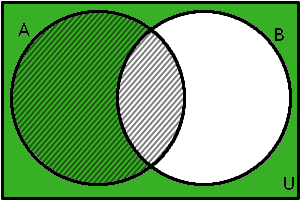
\(A\cup B'\)
Z tohoto obrázku již snadno odvodíme, jaké prvky patří do množiny \(A\cup B'\). Jsou to právě prvky obsažené v množině reprezentované tou částí diagramu, která je zelená nebo šrafovaná. Vidíme, že takto vyznačená je většina diagramu. Proto bude možná vhodné spíše říci, které prvky do \(A\cup B'\) nepatří. To je z diagramu zřejmé, jsou to právě ty prvky množiny \(B\), které zároveň nejsou prvky množiny \(A\). To jsou prvky 1, 2, 3. Všechny ostatní prvky do množiny \(A\cup B'\) patří. Teď už můžeme zapsat, jaké prvky vyšetřovaná množina obsahuje: \(A\cup B'\) = {\(x\) \(\in\) \(\mathbb{N}\); \(x\) > 3}.
Předchozí příklad jsme samozřejmě mohli řešit i bez využití Vennových diagramů a to stejným způsobem (opět bychom si museli uvědomit, jaké jsou prvky množiny \(B'\) a jak dále vypadá ono sjednocení), avšak připravili bychom se o názorný obrázek. Ještě důležitější pro nás tyto diagramy budou, pustíme-li se do složitějších úloh a pokusíme se např. ukázat, že dvě různé kombinace množinových operací ústí v tutéž množinu.
