Rozdíl množin
U doplňku množin jsme byli velmi omezeni podmínkou, kdy jedna množina musela být podmnožinou druhé. Nyní si ukážeme operaci, která je doplňku podobná, avšak toto omezení nemá. Rozdíl množin totiž „ukousne“ z jedné množiny to, co má společné s množinou druhou. Rozdíl množin \(A\) a \(B\) budeme značit \(A\) − \(B\) a jeho definice je:
Rozdíl množin \(A\) a \(B\), který značíme \(A\) − \(B\), je množina, která obsahuje všechny prvky množiny \(A\) s výjimkou těch, jež jsou zároveň prvky množiny \(B\).
Což můžeme říci také jinak: Chceme-li vytvořit množinu \(A\) − \(B\), pak stačí vzít množinu \(A\) a vyjmout z ní prvky, které má společné s množinou \(B\). I zde je zřejmé, že ani rozdíl není komutativní. Grafické znázornění rozdílu může vypadat např. takto:
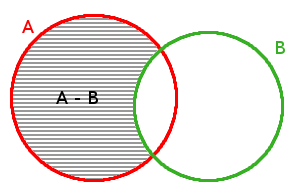 |
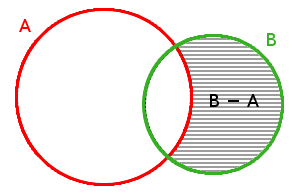 |
| \(A\) − \(B\) | \(B\) − \(A\) |
I rozdíl množin si samozřejmě ukážeme na konkrétních příkladech, měli bychom také poukázat na některé speciální případy:
- Mějme množiny \(A\) = {1, 2, 3, 4, 5, 6} a \(B\) = {1, 3, 6, 8}. Pak je množina \(A \setminus B\) = {2, 4, 5}.
- Jsou-li množiny \(C\) = \(\mathbb{N}\) a \(D\) = {\(x \)\(\in\) \(\mathbb{N}\); \(x\) > 5}. Pak je množina \(C\) − \(D\) = {1, 2, 3, 4, 5}.
- Zkusíme-li provést rozdíl množiny se sebou, získáme prázdnou množinu: \(M\) − \(M\) = \(\emptyset\).
- Jak dopadne rozdíl u dvou množin, které nemají žádné společné prvky? Výsledkem bude původní množina, od které „odečítáme“, protože z ní podle definice rozdílu odebereme všechny prvky, které jsou současně v druhé množině, a těch je nula. Tedy např. bude-li \(A\) = \(\mathbb{N}\) a \(B\) = {0, −1, −2, −3}, pak \(A\) − \(B\) = \(A\) = \(\mathbb{N}\).
- Pokud nastane situace, kdy jedna množina je podmnožinou druhé, mohou nastat dva případy podle toho, jaké pořadí množin zvolíme v rozdílu. Budeme mít dvě množiny \(C\) a \(D\), pro něž platí \(C\) \(\subseteq\) \(D\). Pak \(C\) − \(D\) = \(\emptyset\), protože z \(C\) odebereme všechny její prvky (všechny totiž patří i do množiny \(D\)). Opačný rozdíl je také zajímavý: \(D\) − \(C\) = \(C\)'\(_D\). V tomto speciálním případě se tedy rozdíl chová stejně jako doplněk (z množiny \(D\) totiž odebereme všechny její prvky, které jsou zároveň prvky množiny \(C\)).
- Pro libovolnou množinu \(M\) také platí: \(M \setminus \emptyset\) = \(M\). Prázdná množina neobsahuje žádné prvky, proto nemůže mít žádné prvky společné s množinou \(M\), a tak výsledkem takového rozdílu musí být opět množina \(M\).
Obrazně opět můžeme hovořit o „odstřihnutí“ části množiny, a to konkrétně té části, kterou má společnou s množinou, jíž „odečítáme“.
