Inkluze a rovnost množin
Je-li každý prvek nějaké množiny \(H\) zároveň prvkem nějaké množiny \(M\) (která však může obsahovat i další prvky), pak říkáme, že množina \(H\) je podmnožinou množiny \(M\). Máme-li např. množinu \(M\) = \(\{1, 2, 3, 4, 5, 6\}\) a množinu \(H\) = \(\{1, 3, 4, 5\}\), můžeme říci, že množina \(H\) je podmožinou množiny \(M\). Tuto informaci můžeme zapsat pomocí symbolu \(\subseteq\) takto: „\(H\) \(\subseteq\) \(M\)“. Je dobré si uvědomit, že každá (i prázdná) množina je podmnožinou sebe sama a také že prázdná množina je podmnožinou každé množiny. Vztah „být podmnožinou“ se nazývá inkluze.
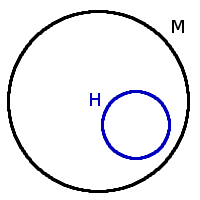
\(H\) \(\subseteq\) \(M\)
Pomocí inkluze se obvykle také zavádí rovnost množin, která se značí obvyklou značkou „=“. Rovnost zavádíme jako tzv. oboustrannou inkluzi, neboli máme-li množiny \(A\) a \(B\), jsou si tyto množiny rovny právě tehdy, když platí \(A \subseteq B\) a současně \(B \subseteq A\), což můžeme zapsat i pomocí výrokové symboliky: \(A = B \Leftrightarrow [A \subseteq B \wedge B \subseteq A] \). Takto zavedená rovnost odpovídá intuitivní představě rovnosti množin – množiny jsou si rovny, pokud obsahují právě tytéž prvky. Pokud bychom chtěli rovnost množin graficky, kruhy reprezentující tyto dvě množiny by se přesně překrývaly.
Protože jsme si již nadefinovali rovnost množin, můžeme si říci, že někdy rozlišujeme ostrou a neostrou inkluzi. Platí mezi nimi vztah podobný ostré a neostré nerovnosti. Neostrá inkluze je právě ten vztah, který jsme si o odstavec výše nadefinovali jako inkluzi. Ostrá inkluze také říká, že množina je podmnožinou nějaké množiny, ale navíc přidává, že si tyto dvě množiny nejsou rovny. Neostrá inkluze tedy rovnost připouští, ostrá nikoli. Chceme-li zapsat ostrou inkluzi, použijeme místo značky \(\subseteq\) značku \(\subset\). U ostré inkluze hovoříme o vlastní podmnožině, u neostré o nevlastní podmnožině.
Máme-li množiny \(A\) = \(\{1, 2, 3, 4, 5, 6\}\), \(B\) = \(\{1, 2, 3, 4, 5, 6\}\) a \(C\) = \(\{1, 2, 3, 4\}\). Pak všechna tato tvrzení platí: \(A \subseteq B\), \(B \subseteq A\), \(C \subseteq A\), \(C \subseteq B\), \(A\) = \(B\), \(C\) \(\subset\) \(A\) a \(C\) \(\subset\) \(B\). Naopak, např. tvrzení \(B\) \(\subset\) \(C\) a \(A \subset C\) pravdivá nejsou.
V předcházejících odstavcích jsme si stručně shrnuli, co už bychom měli o množinách vědět, a ukázali, jaké značení budeme používat. Nyní začněme se zavedením množinových operací – doplňku, rozdílu, sjednocení a průniku.
