Funkce
Pojem funkce je jedním z nejdůležitějších pojmů v matematice. V této práci se pokusíme problematiku funkcí přiblížit středoškolskému studentovi. Budou probrány obecné vlastnosti funkcí, lineární funkce, kvadratické funkce, funkce s absolutními hodnotami, exponenciální a logaritmické funkce, mocninné funkce a lineární lomené funkce. Goniometrické funkce zde probrány nejsou, tato partie je podrobně probrána v jiné práci, viz Goniometrie a trigonometrie.
Použití tlačítek
V celé práci se objevují dva druhy tlačítek:
 | Otazník se obvykle objevuje tam, kde je úkolem vyřešit příklad. Když na něj kliknete, objeví se řešení. |
 | Hvězdička se obvykle objevuje tam, kde je nějaké rozšíření látky. |
Použitá symbolika a značení
Množiny
| \(\{a;b;c\}\) | množina obsahující prvky \(a\), \(b\) a \(c\) |
Číselné množiny
| \(\mathbb N\) | přirozená čísla; tedy {1;2;3;...} |
| \(\mathbb Z\) | celá čísla; tedy {...;-2;-1;0;1;2;...} |
| \(\mathbb Q\) | racionální čísla; taková čísla, která lze zapsat jako \(\frac{p}{q}\), kde \(p\in\mathbb Z\) a \(q\in\mathbb N\) |
| \(\mathbb R\) | reálná čísla |
Intervaly
| \((a;b)\) | otevřený interval, tzn. \(a\), \(b\) nejsou prvky tohoto intervalu |
| \(\langle a;b\rangle\) | uzavřený interval, tzn. \(a\), \(b\) jsou prvky tohoto intervalu |
| \((a;b\rangle\) | zprava uzavřený interval, tzn. \(a\) není prvkem tohoto intervalu a \(b\) je prvkem |
| \(\langle a;b)\) | zleva uzavřený interval, tzn. \(a\) je prvkem tohoto intervalu a \(b\) není prvkem |
Grafy
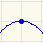 | tento bod leží na grafu funkce |
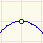 | tento bod neleží na grafu funkce |




