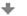Substitúcia na základný typ
Pomocou jednoduchej substitúcie \(y = x +l\) alebo \(y = x\cdot l\) prevedieme zložitejšiu goniometrickú rovnicu typu \(g(x+l) =k\) alebo \(g(x \cdot l)=k\), kde g je goniometrická funkcia s neznámou \(x\) a \(l,k\) sú reálne čísla, na základný typ goniometrických rovníc \(g(y) =k\).
- Príklad 1
- Riešte goniometrickú rovnicu s neznámou \(x \in \mathbb{R}\):
\(\sin 2x = -\frac{1}{2}\)
Riešenie
Zavedieme pomocnú substitúciu \(y=2x\) a dostaneme rovnicu \(\sin y = -\frac{1}{2}\).

Z grafu je vidieť, že pre \(y = \frac{11}{6}{\pi}; \frac{7}{6}{\pi}; -\frac{1}{6}{\pi}; -\frac{5}{6}{\pi}\) je na intervale \(\langle -2\pi;2\pi\rangle\) funkcia \(\sin y = -\frac{1}{2}\).
Využitím periodičnosti funkcie sínus dostávame riešenia:
\(y_1 = \frac{7}{6}{\pi} + 2k\pi; k \in \mathbb{Z}\), a \(y_2 = \frac{11}{6}{\pi} + 2 k\pi; k \in \mathbb{Z}\)
Vrátime sa k substitúcií a postupnou úpravou dostávame:
\(y_1 = \frac{7}{6}{\pi} + 2k\pi\)
\(2x_1 = \frac{7}{6}{\pi} + 2k\pi\) \(/:2\)
\(x_1 = \frac{7}{12}{\pi} + k\pi, ; k \in \mathbb{Z}\) (Prvé riešenie.)
\(y_2 = \frac{11}{6}{\pi} + 2k\pi\)
\(2x_2 = \frac{11}{6}{\pi} + 2k\pi\) \(/:2\)
\(x_2 = \frac{11}{12}{\pi} + k\pi, ; k \in \mathbb{Z}\) (Druhé riešenie.)
Výsledné riešenie môžme zapísať v tvare \(K = \bigcup\limits_{k\in\mathbb{Z}}\{\frac{7}{12}{\pi}+ k\pi;\frac{11}{12}{\pi}+ k\pi\}\;\).
- Príklad 2
- Riešte goniometrickú rovnicu s neznámou \(x \in \mathbb{R}\):
\({\rm tg}\: (4x-3) = 1\)
Platí podmienka: \(4x-3 \not=(2k+1)\frac{1}{2}{\pi}; k \in \mathbb{Z}. \)
\(x \not=\frac{5}{4} + k \frac{\pi}{4}. \)
Zavedieme pomocnú substitúciu \(y=(4x-3)\) a dostaneme rovnicu:
\({\rm tg}\: y=1\)
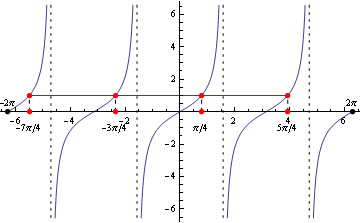
Z grafu a zo základných tabuľkových hodnôt funkcie tangens plynie, že pre \(y =\frac{1}{4}{\pi} +k\pi\ \) je funkcia \({\rm tg}\: y = 1\).
Vrátime sa späť k substitúcii a postupnou úpravou dostávame:
\(y = \frac{1}{4}{\pi} + k\pi\)
\(4x-3= \frac{1}{4}{\pi} + k\pi\) \(/+3\)
\(4x = \frac{1}{4}{\pi} + k\pi +3\)\(/:4\)
\(x = \frac{1}{16}{\pi} + \frac {3}{4} + \frac{k\pi}{4}\)
Výsledné riešenie môžme zapísať v tvare \(K = \bigcup\limits_{k\in\mathbb{Z}}\{\frac{1}{16}{\pi}+ \frac{1}{4}{k\pi}+ \frac{3}{4}\}\;\).