\begin{align}
\end{align}
Riešte rovnice s neznámou
\(t \in \mathbb{R}\):
1.
\(2\sin^2 t + 3\cos t = 0\)
-
\(2(1-\cos^2 t) + 3\cos t = 0\)
(Používame vzorce uvedené v časti goniometrické vzorce. )
-
\(2\cos^2 t - 3 \cos t - 2 = 0\)
- Zavedieme substitúciu:
\(\cos t = y\)
-
\(2y^2 - 3y - 2 = 0\)
(Vypočítame diskriminant kvadratickej rovnice a určíme riešenia rovnice, postupujeme ako vo vzorových príkladoch kapitoly.)
-
\(D=25\)
-
\(y_{1,2}={3\pm 5 \over 4} \Rightarrow y_1 = 2; y_2 = -{1 \over 2}\)
- Vrátime sa k substitúcii
\(\cos t = y\)
a po dosadení za y dostávame:
-
\(\cos t_1 = 2 \Rightarrow t_1 \in \emptyset\)
-
\(\cos t_2 = -{1 \over 2}\)
-

-
\(\cos t_2 = -{1 \over 2} \Rightarrow t_2 = {2 \over 3}\pi + 2k\pi; {4 \over 3}\pi + 2k\pi\)
- Výsledné riešenie napíšeme v tvare:
\(K = \bigcup\limits_{k\in\mathbb{Z}}\{\frac{2}{3}{\pi}+2k\pi; \frac{4}{3}{\pi}+2k\pi \}\;.\)
2.
\(2\sin^2 t -\cos^2 t - 4\sin t +2 = 0\)
3.
\(12\sin^4 t + \sin^2 t - 1 = 0\)
- Zavedieme substitúciu
\(\sin^2 t = y\)
-
\(12y^2 + y - 1 = 0\)
-
\(D=49\)
-
\(y_{1,2}={-1\pm 7 \over 24} \Rightarrow y_1 = -{1 \over 3}; y_2 = {1 \over 4}\)
-
\(\sin^2 t_1 = -{1 \over 3} \Rightarrow t_1 \in \emptyset\)
(Druhá mocnina je nezáporné číslo!)
-
\(\sin^2 t_2 = {1 \over 4} \Rightarrow \sin t_2 = \pm {1 \over 2}\)
-

-
\(\sin t_2 = {1 \over 2} \Rightarrow t_2 = {\pi \over 6} + 2k\pi; {5 \over 6}\pi + 2k\pi, k \in \mathbb{Z}\)
-
\(\sin t_3 = -{1 \over 2} \Rightarrow t_2 = {7 \over 6}\pi + 2k\pi; {11 \over 6}\pi + 2k\pi, k \in \mathbb{Z}\)
- Využitím periodičnosti funkcie sínus dostávame výsledné riešenie, ktoré zapíšeme v tvare:
\(K = \bigcup\limits_{k\in\mathbb{Z}}\{\frac{\pi}{6}+k\pi; \frac{5}{6}{\pi}+k\pi \}\;.\)
4.
\({\rm tg}\: t + {\rm cotg}\: t = 2\)
-
\({\rm tg}\: t + \large{1 \over {\rm tg}\: t} -2 = 0\)
(Používame vzorce uvedené v časti časti.)
- Aby výrazy v rovnici boli definované, musí platiť:
\({\rm tg}\: t \not= (2k + 1)\cdot {\pi \over 2}\)
-
\({\rm tg^2}\: t + 1 - 2{\rm tg}\: t = 0\)
- Zavedieme substitúciu
\({\rm tg}\: t = y\)
-
\(y^2 - 2y + 1 = 0\)
(Vyriešime kvadratickú rovnicu a urćíme korene rovnice.)
-
\(D = 0 \Rightarrow y = {2 \over 2} = 1\)
-
-
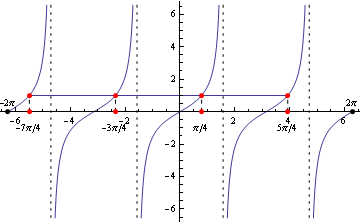
\({\rm tg}\: t = 1 \Rightarrow t = {\pi \over 4} + k\pi\)
(Využívame periodičnosť funkcie tangens.)
- Výsledné riešenie napíšeme v tvare
\(K = \bigcup\limits_{k\in\mathbb{Z}}\{\frac{\pi}{4}+k\pi \}\;.\)
5.
\(2\sin t\ {\rm tg}\: t + 4\cos t -5 = 0\)