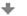Základné goniometrické nerovnice
Riešenie základných goniometrických nerovníc je viditeľné priamo z grafov goniometrických funkcií, ako si to môžme pozrieť na úvodných vzorovo riešených príkladoch. Kapitola obsahuje aj úlohy určené k precvičovaniu, ktoré sú obohatené krokovaným riešenim. Pri riešeni základných goniometrických nerovníc sa predpokladá znalosť riešenia goniometrických rovníc, lineárnych a kvadratických nerovníc.
- Príklad 1
- Riešte goniometrickú nerovnicu s neznámou \(x \in \mathbb{R}\):
\(\cos x > {1 \over 2}\)
Riešenie
Na tomto príklade si ukážeme dve rôzne metody ako riešiť goniometrickú nerovnicu.
Prvá metóda:
V prvom prípade riešenie určíme pomocou jednotkovej kružnice.
Z jednotkovej kružnice je vidieť, že daná goniometrická nerovnica nadobúda riešenie v prvom a v štvrtom kvadrante. Časť jednotkovej kružnice znázornená červenou farbou určuje riešenie danej goniometrickej nerovnice.
Výsledné riešenie môžme zapísať v tvare:
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left ({5\pi \over 3} + 2k\pi; 2\pi + {\pi \over 3} + 2k\pi \right) = \left (-{\pi \over 3} + 2k\pi; {\pi \over 3} + 2k\pi \right),\) využívame podobne ako pri goniometrických rovniciach periodičnosť funkcie kosínus, platí \(-{\pi \over 3} + 2\pi = {5 \over 3}\pi.\)
Druhá metóda:
V druhom prípade riešenie určíme pomocou grafu funkcie kosínus.

\(K = \bigcup\limits_{k\in\mathbb{Z}} \left (-{\pi \over 3} + 2k\pi; {\pi \over 3} + 2k\pi \right).\)
- Príklad 2
- Riešte goniometrickú nerovnicu s neznámou \(x \in \mathbb{R}\):
\({\rm tg}\: x \leq {\large \sqrt {3} \large \over \large 3}\)
Riešenie
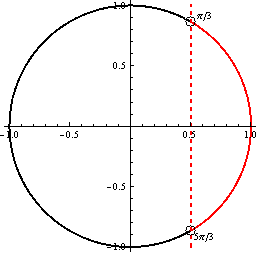
Aby výrazy v nerovnici boli definované, musí platiť podmienka \(x \not= (2k + 1){\large \pi \large \over \large 2}; k \in \mathbb{Z}.\)
Z jednotkovej kružnice je vidieť, že riešenim je množina
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left (-{\pi \over 2} + k\pi; {\pi \over 6} + k\pi \right \rangle \), , pričom platí, že v bode \(-{\pi \over 2}\) funkcia tangens nie je definovaná, preto použijeme okrúhlu zátvorku, naopak bod \({\pi \over 6}\) patrí do riešenia, plynie zo zadania, preto použijeme uhlovú zátvorku.
- Príklad 3
- Riešte goniometrickú nerovnicu s neznámou \(x \in \mathbb{R}\):
\(0 \leq {\rm cotg}\: x \leq \sqrt {3}\)
Riešenie
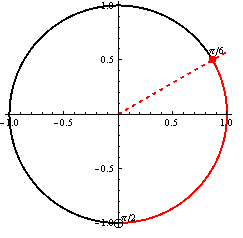
Aby výrazy v nerovnici boli definované, musí platiť podmienka \(x \not= (k\pi; k \in \mathbb{Z}.\)
Využitím grafu a periodičnosti funkcie kotangens dostávame výsledok, ktorý zapíšeme v tvare
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left \langle -{\pi \over 3} + 2k\pi; {\pi \over 3} + 2k\pi \right \rangle.\)