Konvexnost a konkávnost - úvod
V této kapitole se naučíte určovat intervaly ryzí konvexnosti a ryzí konkávnosti a nalézat inflexní body různých funkcí. Následující příklad neformálně ukazuje rozdíl mezi ryze konvexní a ryze konkávní funkcí.
Ilustrace 1
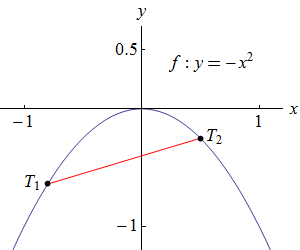 |
 |
Na obrázku vlevo je graf funkce \(f\) nad úsečkou \(T_1 T_2\) s výjimkou krajních bodů. Graf funkce by byl nad touto úsečkou, i kdybychom zvolili jakékoliv jiné dva různé body \(T_1\) a \(T_2\) ležící na grafu dané funkce. Taková funkce se nazývá ryze konkávní.
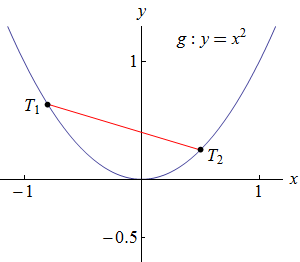
Naproti tomu na obrázku vpravo je graf funkce \(g\) pod úsečkou \(T_1 T_2\) s výjimkou krajních bodů. Graf funkce by byl pod touto úsečkou, i kdybychom zvolili jakékoliv jiné dva různé body \(T_1\) a \(T_2\) ležící na grafu dané funkce. Taková funkce se nazývá ryze konvexní.
Ilustrace 2
Možná Vás napadne otázka, jak může vypadat funkce, která je konvexní, ale není ryze konvexní.
Konvexní funkce je taková funkce, jejíž graf leží pod úsečkou \(T_1 T_2\) nebo na této úsečce pro libovolné dva různé body \(T_1\) a \(T_2\) ležící na grafu funkce.
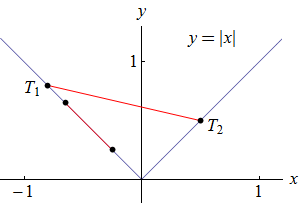
Funkce \(y = |x|\) je konvexní, ale není ryze konvexní, jak objasňuje následující obrázek.
Ilustrace 3
Existují funkce, které jsou současně konvexní i konkávní. Těmito funkcemi jsou lineární funkce. Jejich grafem je přímka.