Monotónnost a extrémy - úvod
V této kapitole se naučíte určovat intervaly monotónnosti a nalézat maxima a minima různých funkcí. Maxima a minima nazýváme souhrnně extrémy. Rozlišujeme lokální a globální extrémy. Následující příklad neformálně ukazuje rozdíl mezi lokálním a globálním maximem.
Ilustrace
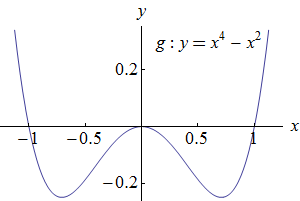
Na následujících obrázcích jsou zobrazeny grafy funkcí \(f: y = -x^2\) a \(g: y = x^4-x^2\), jejichž definičním oborem je množina všech reálných čísel. Předpokládejme, že hledáme maxima na této množině.
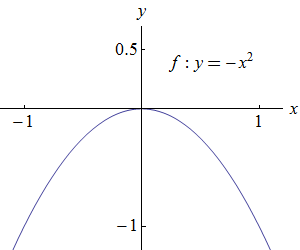 |
 |
Pro funkci \(f\), jejíž graf je zobrazen na obrázku vlevo, platí, že \(f(x) \leq 0\) pro všechna \(x \neq 0\). Nejvyšší - maximální hodnotou funkce \(f\) na množině všech reálných čísel je nula v bodě \(x = 0\). V tomto bodě má funkce své maximum. Hodnotou tohoto maxima je \(f(0) = -0^2 = 0\), tedy nula. Protože neexistují žádné body z definičního oboru funkce \(f\), v nichž by funkce \(f\) nabývala vyšších hodnot, tak se toto maximum nazývá globální maximum.
Naproti tomu pro funkci \(g\), jejíž graf je zobrazen na obrázku vpravo, neplatí, že by bylo \(g(x) \leq 0\) pro všecha \(x \neq 0\). Například \(0 = g(0) \lt g(2) = 12\). Proto funkce \(g\) nenabývá v bodě \(x = 0\) globální maximum. Vidíme však, že existuje okolí bodu \(x = 0\), na kterém nabývá funkce \(g\) maximum. Tímto okolím je například interval \((-0.5,0.5)\). Proto se toto maximum nazývá lokální maximum. Hodnotou tohoto maxima je \(g(0) = 0^4-0^2 = 0\), tedy opět nula.
Mezi globálními a lokálními extrémy platí tento vztah: každý globální extrém je lokálním extrémem. Jak jsme však viděli na funkci \(g\), ne každý lokální extrém je globálním extrémem. Opačný vztah tedy neplatí.
