\begin{align}
\end{align}
Skalární součin
Umíme sčítat a odečítat vektory, násobit je reálným číslem i vypočítat jejich velikost. Další operace, kterou si zavedeme, se nazývá skalární součin a umožní nám násobit vektory mezi sebou.
Definice
Skalární součin dvou vektorů u = (u1; u2), v = (v1; v2) v rovině je číslo u1v1 + u2v2.
Skalární součin dvou vektorů u = (u1; u2; u3), v = (v1; v2; v3) v prostoru je číslo u1v1 + u2v2 + u3v3.
Skalární součin vektorů u a v zapisujeme jako uv nebo u·v.
Poznámka
Všiměte si, že výsledkem skalárního součinu dvou vektorů je číslo. Ukážeme si, jak se dá skalární součin využít a co nám říká o vzájemném vztahu vektorů, které mezi sebou násobíme.
Úmluva: Místo uu budeme psát u2.
Příklad 2.9
Vypočítejte skalární součin vektorů u = (1; -2) a v = (2; -3).
Řešení
- uv = 1∙2 + (-2)∙(-3) = 2 + 6 = 8
Úloha
Pro u = (-5; 5) a v = (-2; -2) vypočítejte uv.
- uv = (-5)⋅(-2) + 5⋅(-2)
- uv = 0
Věta
Pro každé vektory u, v, w (v rovině i v prostoru) a každé reálné číslo r platí:
- uv = vu;
- (ru)v = r(uv);
- w(u + v) = wu + wv.
Ukážeme si, jak bychom tato tvrzení dokazovali v prostoru. Nechť u = (u1; u2; u3), v = (v1; v2; v3), w = (w1; w2; w3) a r je libovolné reálné číslo.
1.
uv = (u1; u2; u3)⋅(v1; v2; v3) = u1v1 + u2v2 + u3v3,
vu = (v1; v2; v3)⋅(u1; u2; u3) = v1u1 + v2u2 + v3u3,
Z komutativity součinu reálných čísel plyne rovnost u1v1 + u2v2 + u3v3 = v1u1 + v2u2 + v3u3 a tedy uv = vu.
2.
(ru)⋅v = (r(u1; u2; u3))⋅(v1; v2; v3) = (ru1; ru2; ru3)⋅(v1; v2; v3) = (ru1)v1 + (ru2)v2 + (ru3)v3,
r⋅(uv) = r((u1; u2; u3)⋅(v1; v2; v3)) = r(u1v1 + u2v2 + u3v3) = r(u1v1) + r(u2v2) + r(u3v3),
Znovu využijeme komutativity součinu reálných čísel, ze které plyne, že (ru1)v1 + (ru2)v2 + (ru3)v3 = r(u1v1) + r(u2v2) + r(u3v3), tedy (ru)v = r(uv).
3.
w(u + v) = (w1; w2; w3)⋅((u1; u2; u3) + (v1; v2; v3)) = (w1; w2; w3)⋅(u1 + v1; u2 + v2; u3 + v3) = w1(u1 + v1) + w2(u2 + v2) + w3(u3 + v3) = w1u1 + w1v1 + w2u2 + w2v2 + w3u3 + w3v3,
wu + wv = (w1; w2; w3)⋅(u1; u2; u3) + (w1; w2; w3)⋅(v1; v2; v3) = w1u1 + w2u2 + w3u3 + w1v1 + w2v2 + w3v3.
Prozkoumáním získaných rovností se snadno přesvědčíme, že w(u + v) = wu + wv.
Odchylka dvou vektorů
Definice
Mají-li dva nenulové vektory u, v umístění OU, OV, nazývá se velikost konvexního úhlu UOV odchylka vektorů u, v. Jsou-li přímky OU, OV navzájem kolmé, říkáme, že i vektory u, v jsou navzájem kolmé.
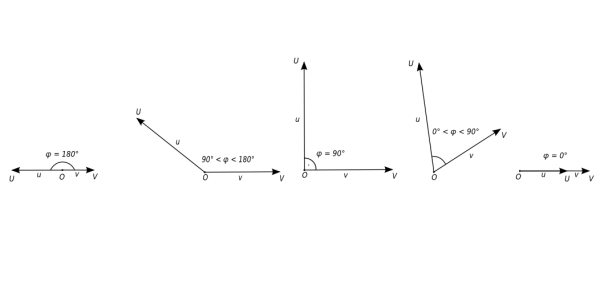
Obr. 2.5: Odchylka vektorů
Poznámka
V případě, že je alespoň jeden vektor nulový, odchylku nedefinujeme.
Věta
Pro dva nenulové vektory u, v v rovině nebo v prostoru a jejich odchylku φ platí:
uv = |u|⋅|v| cos φ, φ ∈ <0°; 180˚>.
V rovině bychom větu dokázali takto. Zvolíme si kartézskou soustavu souřadnic Oxy tak, aby polopřímka OU byla kladná poloosa x a bod V ležel v polorovině, která obsahuje kladnou poloosu y a má hraniční přímku x. Nyní můžeme určit souřadnice vektorů u, v pomocí jejich velikosti a úhlu φ: u = (|u|; 0), v = (|v|cos φ; |v|sin φ). Potom platí uv = |u|⋅|v|cos φ.
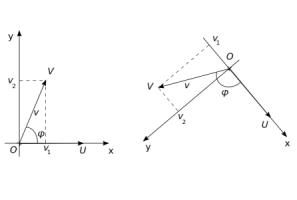
Obrázek k důkazu
Poznámka
Pro výpočet odchylky dvou nenulových vektorů u, v můžeme použít vzorec vyplývající z předchozí věty. Později tento vzorec využijeme například pro určování odchylek dvou přímek:
\(\cosφ = \dfrac{uv}{|u||v|}, φ \in \langle 0°;180° \rangle\).
Věta
Pro každé dva vektory u,v v rovině nebo v prostoru platí, že uv = 0 právě tehdy, když je alespoň jeden z vektorů je nulový vektor nebo když jsou oba dva vektory nenulové a navzájem kolmé.
Z definice skalárního součinu plyne, že jestliže u nebo v je nulový vektor, pak i uv = 0.
Pokud jsou oba dva vektory nenulové, tak podle předchozí věty platí uv = |u||v| cos φ. Protože |u| i |v| jsou nenulové, tak uv = 0 právě tehdy, když cos φ = 0. To nastává právě v tom případě, kdy je odchylka φ = 90°, tj. vektory u a v jsou na sebe kolmé. Je potřeba si uvědomit, že odchylka dle definice musí ležet v intervalu <0°; 180°>.


