\begin{align} \end{align}

Vzdálenost

V rovině jsme počítali vzdálenost bodu od přímky a vzdálenost dvou přímek. V prostoru se naučíme řešit tytéž úlohy a navíc budeme počítat vzdálenost bodu od roviny a vzdálenost dvou rovin.

Vzdálenost bodu od přímky

Mějme zadánu přímku p(A, u) a bod B. Hledáme vzdálenost d bodu B od přímky p viz obr. 4.10.

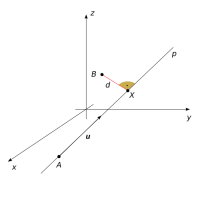
Obr. 4.10: Vzdálenost bodu od přímky
Obr. 4.10: Vzdálenost bodu od přímky

Najdeme takový bod X přímky p, pro který platí (B - X)u = 0. Že to musí platit je zřejmé z obrázku a je i vidět, že takový bod je jen jeden. Vzdálenost bodu B od přímky p je potom rovna |XB|.

Úmluva: Stejně jako v rovině budeme vzdálenost bodu B od přímky p značit |Bp|.

Příklad 4.9

Určete vzdálenost bodu B od přímky p(A, u), je-li A[3; 0; -1], B[1; 2; 1] a u = (-1; 0; 1).

Řešení
  • Jak jsme si vysvětlili, hledáme nejprve bod X[x; y; z], který bude ležet na přímce p a pro který platí, (B - X)u = 0. Protože bod X leží na přímce p, můžeme s využitím jejího parametrického vyjádření jeho souřadnice zapsat jako:
    x = 3 - t,
    y = 0,
    z = -1 + t,
    pro nějakou hodnotu parametru t. Vyjádříme druhou podmínku, (B - X)u = 0:
    (1 - 3 + t)⋅(-1) + (2 - 0)⋅0 + (1 + 1 - t)⋅1 = 0,
    2 - t + 2 - t = 0,
    t = 2.
  • Zjistili jsme, že bod X má souřadnice X[1; 0; 1]. Vzdálenost d, bodu B od přímky p, je rovna
    \(|d| = |Bp| = |XB| = \sqrt{0^{2} + 2^{2} + 0^{2}} = 2\).
  • Celý příklad by se dal řešit ještě jinak. Bodem B můžeme vést rovinu kolmou na přímku p. Ta přímku p protne v nějakém bodě Y. Vzdálenost |BY| je vzdálenost bodu B od přímky p.
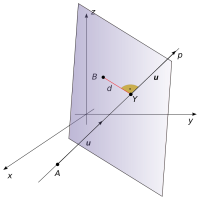    Obr. 4.11: Řešení příkladu 4.9
    Obr. 4.11: Řešení příkladu 4.9
  • Normálový vektor roviny kolmé na přímku p je směrovým vektorem přímky p, tedy u = (-1; 0; 1). Její obecná rovnice je -x + z + d = 0. Koeficient d určíme po dosazení souřadnic bodu B do této rovnice, d = 0. Hledáme bod Y, který je průsečíkem roviny -x + z = 0 a přímky p:
    -(3 - t) + (-1 + t) = 0,
    -3 + t - 1 + t = 0,
    2t - 4 = 0,
    t = 2.
  • Bod Y má souřadnice Y[1; 0; 1]. Všiměte si, že body X a Y jsou ve skutečnosti jeden a tentýž bod:
    \(|d| = |YB| = \sqrt{0^{2} + 2^{2} + 0^{2}} = 2\).

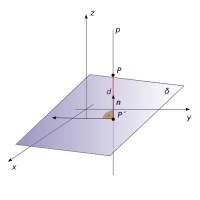
Vzdálenost bodu od roviny

Věta

Vzdálenost d bodu P[p1; p2; p3] od roviny δ: ax + by + cz + e = 0 je vyjádřena vzorcem:

\(d = \dfrac{|ap_{1} + bp_{2} + cp_{3} + e|}{\sqrt{a^{2} + b^{2} + c^{2}}}\).

zobraz důkaz

Úmluva: Vzdálenost bodu B od roviny ρ budeme značit |Bρ|.

Úloha

Spočítejte vzdálenost bodu B[1; -5; 5] od roviny ρ: x + 6y + 2z + 3 = 0.

Řešení