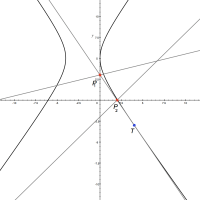
Vzájemná poloha hyperboly a přímky
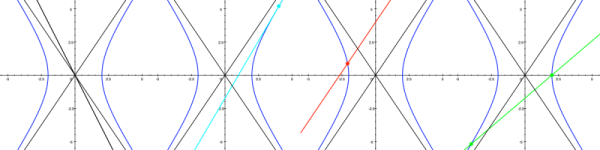
V rovině mohou nastat tři různé vzájemné polohy hyperboly H a přímky p: nemají žádný společný bod, mají jeden společný bod nebo mají dva společné body.
- p ∩ H = ∅
Přímka p nemá s hyperbolou H žádný společný bod. - p ∩ H = {T}
Přímka p má s hyperbolou H právě jeden společný bod, bod T.
- Pokud je přímka p různoběžná s asymptotami hyperboly, nazýváme ji tečnou hyperboly H.
- Pokud je přímka p rovnoběžná s některou z asymptot hyperboly H, tečnou jí nenazýváme.
- Pokud je přímka p různoběžná s asymptotami hyperboly, nazýváme ji tečnou hyperboly H.
- p ∩ H = {X, Y}
Přímka hyperbolou prochází a protíná ji v bodech X a Y. Přímku p nazýváme sečnou hyperboly H.
- Z rovnice přímky vyjádříme x = 1 - 3y a dosadíme do rovnice hyperboly: \(\dfrac{(1 - 3y + 2)^{2}}{9} - \dfrac{(y - 1)^{2}}{4} = 1\).
- Získanou kvadratickou rovnici upravíme na
4(9y2 - 18y + 9) - 9(y2 - 2y + 1) = 36,
3y2 - 6y - 1 = 0. - Z diskriminantu této rovnice určíme počet jejích řešení a tím zároveň počet průsečíků hyperboly H a přímky p.
D = 36 - 4⋅3⋅(-1) = 48.
D > 0, rovnice má dvě různá řešení. To znamená, že hyperbola H a přímka p mají dva společné body.
Je dána přímka p: 4x - 15y - 4 = 0 a hyperbola H: \(\dfrac{(x - 1)^{2}}{81} - \dfrac{y^{2}}{9} = 1\). Určete jejich vzájemnou polohu a společné body, pokud existují.
- Podobně jako v příkladě 5.20 si nejprve z rovnice přímky p vyjádříme x: \(x = \dfrac{15y + 4}{4}\).
- Dosadíme do rovnice hyperboly H a řešíme kvadratickou rovnici:
\(\dfrac{\left(\dfrac{15y + 4}{4} - 1\right)^{2}}{81} - \dfrac{y^{2}}{9} = 1\),
\(\dfrac{\left(\dfrac{15y}{4}\right)^{2}}{81} - \dfrac{y^{2}}{9} = 1\),
\(\dfrac{225y^{2}}{16} - 9y^{2} = 81\),
81y2 = 896,
y2 = 16,
y1, 2 = ±4. - Rovnice má dvě řešení, proto je přímka p sečnou hyperboly H. Jejich průsečíky jsou body P1[16; 4] a P2[-14; 4], jejichž x-ové souřadnice získáme dosazením hodnot y1, 2 do rovnice přímky p.
\(\dfrac{(x - m)^{2}}{a^{2}} - \dfrac{(y - n)^{2}}{b^{2}} = 1\) v bodě X0[x0; y0].
Napište rovnici tečny hyperboly 4x2 - 5y2 - 24x - 20y - 4 = 0 v jejím bodě T[8; -6].
- Obecnou rovnici hyperboly převedeme na rovnici středovou:
4(x2 - 6x + 9 - 9) - 5(y2 + 4y + 4 - 4) = 4,
4(x - 3)2 - 5(y + 2)2 - 36 + 20 = 4,
4(x - 3)2 - 5(y + 2)2 = 20,
\(\dfrac{(x - 3)^{2}}{5} - \dfrac{(y + 2)^{2}}{4} = 1\). - Rovnici tečny hyperboly v bodě T určíme z dokázané věty. Je to:
\(\dfrac{(x - 3)(8 - 3)}{5} - \dfrac{(y + 2)(-6 + 2)}{4} = 1\), - x + y - 2 = 0.
Najděte průsečíky tečny hyperboly H:
\(\dfrac{(x + 2)^{2}}{4} - \dfrac{(y - 5)^{2}}{8} = 1\)
v bodě T[4; -3] s přímkami p: x - 4y + 12 = 0 a q: -x + y + 2 = 0.