Analytická geometrie

Určete, zda je vektor u = (2; 1; 6) lineární kombinací vektorů v = (1; -2; 3) a w = (3; 5; 0).

• Je-li náš zadaný vektor u lineární kombinací dvou vektorů v, w, pak existují reálná čísla a, b tak, že u = av + bw. Vektory se rovnají, jsou li stejné jejich souřadnice, hledáme tedy reálná čísla a a b taková, aby platilo (2; 1; 6) = a(1; -2; 3) + b(3; 5; 0). Tedy:
  2 = a + 3b,
  1 = -2a + 5b,
  6 = 3a.
  
• Z poslední rovnice vyjádříme a = 2. Po dosazení do rovnice první, dopočítáme b = 0. Nyní je třeba dosadit spočtené hodnoty do rovnice druhé, abychom ověřili, zda je i tato splněna.
• Získáme
  1 = -2⋅2 + 5⋅0,
  1 ≠ -4.
  Soustava tedy nemá řešení a vektor u není lineární kombinací vektorů v a w.

Vypočítejte velikost vektoru u = (-5; 5). Výsledek zaokrouhlete na dvě desetinná místa.

• \(|u| = \sqrt{(-5)^{2} + 5^{2}} = \sqrt{25 + 25} = \sqrt{50} \approx 7,07.\)

Pro u = (-1; -1) a v = (-2; 6) vypočítejte uv.

• uv = (-1)⋅(-2) + (-1)⋅6
• uv = -4

Pro u = (8; -8; -5) a v = (-8; 0; -4) vypočítejte u × v.

• u × v = ((-8)⋅(-4) - (-5)⋅0; (-5)⋅(-8) - 8⋅(-4); 8⋅0 - (-8)⋅(-8))
• u × v = (32; 72; -64)

Vypočítejte odchylku přímek p: 7x - 2y - 9 = 0 a q: 2x - 8y + 8 = 0. Výsledek zaokrouhlete na stupně.

• K výpočtu odchylky můžeme namísto směrových vektorů použít i vektory normálové, které vidíme v obecných rovnicích přímek p a q.
  np = (7; -2), nq = (2; -8).
• Dosadíme do vzorce a spočítáme cosφ
  \(\cosφ = \dfrac{|7\cdot2 + (-2)\cdot(-8)|}{\sqrt{7^{2} + (-2)^{2}} \cdot \sqrt{2^{2} + (-8)^{2}}} = \dfrac{|30|}{\sqrt{3604}} \approx 0,50\)
• φ ≈ 60°

Určete vzdálenost d přímky p určené body P[1; -4], Q[6; 8] od bodu A[3; 6].

• Nejprve vyjádříme přímku p její obecnou rovnicí. Určíme její směrový vektor u a z něj potom normálový vektor n.
  u = PQ = (5; 12),
  n = (12; -5).
• Obecná rovnice přímky p má tvar:
  12x - 5y + c = 0.
  Dosadíme souřadnice bodu P a dopočítáme hodnotu c:
  12⋅1 -5⋅(-4) + c = 0,
  12 + 20 + c = 0,
  c = -32.
  Obecná rovnice přímky p tedy vypadá takto:
  12x - 5y - 32 = 0.

• Pro výpočet vzdálenosti bodu A od přímky p nám stačí jen dosadit do známého vzorce \(d = \dfrac{|ap_{1} + bp_{2} + c|}{\sqrt{a^{2} + b^{2}}}\).

  \(d = |AP| = \dfrac{|12 \cdot 3 - 5 \cdot 6 - 32|}{\sqrt{12^{2} + (-5)^{2}}} = \dfrac{26}{13} = 2\).

Určete průsečík přímek AB a CD, kde A[1; 0], B[3; 2], C[-1; 5], D[3; 2].

• Úlohu vyřešíme paralelně s využitím parametrického vyjádření přímky v jednom sloupci a s pomocí obecné rovnice přímky ve sloupci druhém. Směrové vektory přímek AB a CD budeme označovat uAB a uCD, normálové potom nAB a nCD.

• Parametrické vyjádření uAB = (2; 2), uCD = (4; -3).

  Obecná rovnice nAB = (2; -2), nCD = (3; 4).

• Určení přímky AB: x = 1 + 2t, y = 2t; t ∈ . Určení přímky CD: x = -1 + 4q, y = 5 - 3q; q ∈ .

  Určení přímky AB: 2x - 2y + c = 0. Po dosazení souřadnic bodu A a získáme 2 + c = 0 ⇒ c = -2, AB: 2x - 2y - 2 = 0, AB: x - y - 1 = 0. Určení přímky CD: 3x + 4y + d = 0. Dosadíme souřadnice bodu C a spočteme d: -3 + 20 + d = 0, d = -17. CD: 3x + 4y - 17 = 0.

• P = AB ∩ CD Hledání průsečíku odpovídá řešení soustavy: 1 + 2t = -1 + 4q, 2t = 5 - 3q. V druhé rovnici vyjádřené 2t dosadíme do první: 1 + 5 - 3q = -1 + 4q, q = 1. Hodnota parametru q = 1 odpovídá v parametrickém vyjádření přímky CD souřadnicím bodu P. Dosadíme a získáme: P = [3; 2].

  P = AB ∩ CD Hledání průsečíku odpovídá řešení soustavy: x - y - 1 = 0, 3x + 4y - 17 = 0. Řešením této soustavy je x = 3 a y = 2, tedy P = [3; 2].

Určete zda bod A[4; 3] leží ve stejné polorovině určené hraniční přímkou p: 2x - y + 3 = 0 a bodem C[1; 2].

• Každá přímka dělí rovinu na dvě poloroviny. Dosadíme-li do levé části obecné rovnice přímky souřadnice nějakého bodu roviny, získáme buď kladné číslo, záporné číslo nebo nulu. Nulu získáme, pokud bod leží na přímce. Po dosazení souřadnic bodů jedné ze zmíněných polorovin, dostaneme kladné číslo. Pokud to budou body druhé poloroviny, bude to číslo záporné.
• Dosadíme-li souřadnice bodu C, získáme hodnotu 2 - 2 + 3 = 3. To je kladné číslo.
• Pokud dosadíme souřadnice bodu A, získáme hodnotu 8 - 3 + 3 = 8. To je také kladné číslo. Na základě našich úvah můžeme říci, že body A a C leží ve stejné polorovině.

Určete, zda bod D[6; 7] leží v úhlu BAC, A[-1; 1], B[-1; 2], C[2; 2].

• Budeme postupovat podobně jako v předchozí úloze. Přímky AB a AC rozdělují rovinu do čtyř částí. Přímku AB nazveme p a přímku AC nazveme q.
• Vyjádříme přímky p a q:
  p: x + 1 = 0,
  q: x - 3y + 4 = 0.
• Teď využijeme znalostí, které jsme získali při řešení předchozí úlohy. Na obrázku je vidět, jaké čísla bychom měli získat po dosazení souřadnic nějakého bodu do levých stran obecných rovnic přímek p a q. Aby takový bod ležel v daném úhlu, musely by nám jeho souřadnice dosazené do levé strany rovnice přímky p dát nezápornou hodnotu. U rovnice přímky q to musí být hodnota nekladná.
  
  

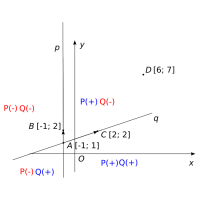
  Obrázek k úloze
• Pokud dosadíme souřadnice bodu C zjistíme, že v případě přímky p získáme číslo 7 a z rovnice přímky q číslo -11. To odpovídá našim požadavkům a můžeme tedy říci, že bod D leží v úhlu BAC.

Najděte bod souměrně sdružený k bodu A[1; 0] podle osy o: x - 2y + 4 = 0.

• Hledaný bod A' leží na kolmici k ose o, která prochází bodem A. Budeme tedy hleda rovnici této kolmice. Její směrový vektor je normálovým vektorem osy o: no = (1; -2). Parametrické vyjádření hledané kolmice, kterou nazveme p, vypadá následovně: p:
  x = 1 + t,
  y = -2t; t ∈ .
• Hledejme dál průsečík přímky p a osy o, prohlédněte si situaci na obrázku.
  
  

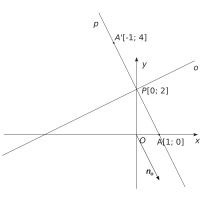
  Obrázek k úloze
• P = p ∩ o,
  1 + t + 4t + 4 = 0,
  5t + 5 = 0,
  t = -1,
  tedy P[0; 2].
• Bod P leží v polovině úsečky AA', kde A' je hledaný obraz bodu A. Jak určit souřadnice středu úsečky již víme a protože známe i souřadnice bodu P, stačí ze vzorce vyjádřit souřadnice hledaného bodu A'.
  \(S_{AA'} = \left[\dfrac{x_{A} + x_{A'}}{2}; \dfrac{y_{A} + y_{A'}}{2}\right] = P\).
  Dosadíme a získáme:
  \(0 = \dfrac{1 + x_{A'}}{2} ⇒ x_{A'} = -1\),
  \(2 = \dfrac{0 + y_{A'}}{2} ⇒ y_{A'} = 4\).
• Hledaný bod A' má souřadnice [-1; 4].