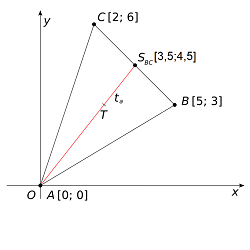
Každou přímku lze zapsat nějakým parametrickým vyjádřením a každé parametrické vyjádření popisuje nějakou přímku.
V minulé kapitole jsme se zabývali vektory, jejich souřadnicemi a operacemi s nimi. Vektory a body budou naše stavební základy, na kterých vystavíme další geometrické útvary jako jsou například přímka a rovina. V této kapitole se budeme věnovat geometrii v rovině a základním geometrickým objektům jako je úsečka, polopřímka a přímka.
Parametrické vyjádření přímky
Parametrické vyjádření přímky je jednou z možností, jak matematicky popsat přímku. Každá přímka v rovině je určena dvěma různými body A a B. Tyto body určují také vektor. My tento vektor pojmenujeme a využijeme jej pro zavedení parametrického vyjádření přímky.
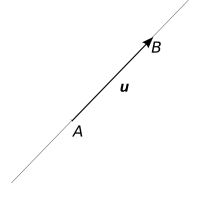
Jestliže A, B jsou dva různé body, pak vektor u = B - A nazýváme směrový vektor přímky AB.
Odpovězte na následující otázky:
- Kolik můžeme najít dvojic bodů, jenž určují stejnou přímku?
- Kolik má přímka směrových vektorů (jak spolu souvisejí)?
- Existuje přímka, jejímž směrovým vektorem je nulový vektor?
- Mohou mít dvě různé přímky stejný směrový vektor? Jak spolu takové přímky souvisejí?
- Na obr. 3.2 určují všechny dvojice bodů AD, BC, DC, CA stejnou přímku. Takových dvojic ale můžeme najít nekonečně mnoho.
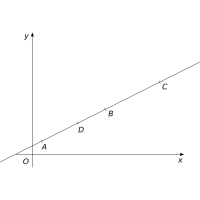 Obr. 3.2: Určení přímky dvojicí bodů
Obr. 3.2: Určení přímky dvojicí bodů - Má jich nekonečně mnoho a každý z nich je reálným násobkem jiného. To plyne z odpovědi na 1. otázku.
- Taková přímka neexistuje. Z definice směrového vektoru plyne, že je nenulový - je určen dvojicí různých bodů.
- Ano mohou. Jsou rovnoběžné různé. Na obr. 3.3 je vidět, že vektory AB a CD jsou různými umístěními vektoru u a oba jsou směrovými vektory různých přímek AB a CD.
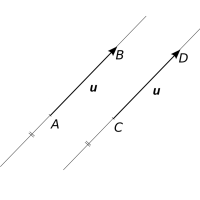 Obr. 3.3: Směrové vektory rovnoběžných přímek
Obr. 3.3: Směrové vektory rovnoběžných přímek
Rovnice
X = A + tu; t ∈ ![]() , u ≠ o
, u ≠ o
se nazývá parametrická rovnice nebo také parametrické vyjádření přímky určené bodem A a
směrovým vektorem u. Proměnná t se nazývá parametr.
Úmluva: Přímku p, určenou bodem P a vektorem u, budeme zapisovat jako p(P, u).
Když parametrickou rovnici přímky p(A, u), kde A[a1; a2] a u = (u1; u2), zapíšeme pomocí souřadnic, získáme vyjádření souřadnic bodů X[x; y] této přímky v závislosti na parametru t.
x = a1 + tu1,
y = a2 + tu2; t ∈ ![]() .
.
Určete parametrické vyjádření přímky zadané body A[2; 1] a B[3; 3].
- Jeden směrový vektor u přímky AB vypočítáme snadno jako u = AB:
u = (3 - 2; 3 - 1),
u = (1; 2). - Podle definice je potom parametrické vyjádření přímky AB:
x = 2 + t,
y = 1 + 2t; t ∈ .
.
Postupným dosazením různých hodnot za parametr t do parametrické rovnice přímky, získáme souřadnice různých bodů této přímky. V příkladě 3.2 hodnotě parametru t = 1 odpovídá bod B, pro hodnotu t = 0 parametrické vyjádření určuje bod A.
Parametrická rovnice přímky je určena volbou jednoho bodu a nějakého směrového vektoru dané přímky. Každá přímka má nekonečně mnoho různých parametrických vyjádření.
Zjistěte, zda bod P[-3; 5] leží na přímce AB, kde A[1; 1] a B[5; -3].
- Nejprve vypočítáme směrový vektor přímky AB a pomocí něj určíme parametrické vyjádření:
u = B - A,
u = (5 - 1; -3 - 1),
u = (4; -4). - Parametrické vyjádření přímky AB vypadá tedy takto:
x = 1 + 4t, (3.1)
y = 1 - 4t; t ∈ .
. - Aby bod P ∈ AB, jeho souřadnice musí splňovat parametrické vyjádření přímky p, tj. musí existovat nějaká hodnota parametru t, která je řešením soustavy:
-3 = 1 + 4t,
5 = 1 - 4t. - Z první rovnice získáme t = -1. Po dosazení do druhé rovnice ověříme, že t = -1 je řešením naší soustavy. Bod P proto leží na přímce AB. V parametrické rovnici (3.1) přímky AB je bod P určený hodnotou parametru t = -1.
- Toto řešení je správné, ale příklad by šel vyřešit o něco rychleji. Stačí si uvědomit, že bod P leží na přímce AB právě tehdy, když je vektor AP reálným násobkem vektoru AB. To bychom v tomto případě mohli rozsoudit pouhým nahlédnutím.
AP = (-4; 4), tj. AP = -1⋅AB.
BP = (-8; 8); je vidět, že BP = -2⋅AB, tedy bod P na přímce AB leží.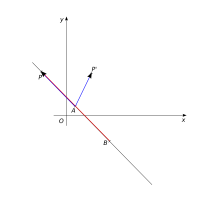 Obr. 3.4: Obrázek k příkladu 3.3
Obr. 3.4: Obrázek k příkladu 3.3
Body, které neleží na jedné přímce se označují jako nekolineární. Naproti tomu body, které na jedné přímce leží se označují jako kolineární.
Určete, jaký geometrický útvar určuje parametrické vyjádření X = A + tu, jestliže
- t ∈ <0; 1>.
- t ∈ <0; ∞).
- Je to úsečka s krajními body A, B, kde B = A + u.
- Určuje polopřímku AB, kde B = A + u.