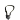Analytická geometrie

Určete obecnou a parametrickou rovnici roviny ρ, která je dána body A[2; 1; 3], B[-1; 2; -1], C[3; 4; 2].

• Nejprve určíme parametrickou rovnici této roviny. K tomu nám stačí znát jeden bod roviny a dva její vektory (přičemž jeden nesmí být reálným násobkem druhého). Bod A známe, určíme tedy vektory u = AB a v = AC:
  u = (-3; 1; -4),
  v = (1; 3; -1).
• Parametrickou rovnici roviny ρ zapíšeme jako:
  x = 2 - 3t + s,
  y = 1 + t + 3s,
  z = 3 - 4t - s; t, s ∈ .
• K určení obecné rovnice musíme znát normálový vektor této roviny. Ten získáme jako vektorový součin vektorů u a v:
  n = u × v = (11; -7; -10).
• Obecná rovnice roviny ρ je
  11x - 7y - 10z + d = 0.
  Po dosazení souřadnic bodu A do této rovnice, dopočítáme d = 15. Obecná rovnice roviny ρ je
  11x - 7y - 10z + 15 = 0.

Určete obecnou rovnici roviny ρ, která prochází bodem B[3; 2; -3] a která je kolmá na přímku x = 1 - t, y = 2 + 2t, z = -t; t ∈ .

• Rovina, která je kolmá na přímku má normálový vektor roven směrovému vektoru této přímky. V našem případě je normálovým vektorem roviny vektor (-1; 2; -1). Rovnici roviny pak můžeme psát jako:
  -x + 2y - z + d = 0.
• Po dosazení souřadnic bodu B, který v rovině leží, dopočítáme d = - 4 a můžeme psát
  ρ: -x + 2y - z - 4 = 0,
  ρ: x - 2y + z + 4 = 0.

Napište parametrickou rovnici roviny ρ, která obsahuje přímky p(A, u) a q(B, v), je-li A[-2; 1; 0], B[-3; 5; 1], u = (1; -1; -1) a v = (-3; 2; 3).

• Přímky p a q určují rovinu, jen pokud nejsou mimoběžné, nebo totožné. Pokud zjistíme, že přímky p a q jsou rovnoběžné různé, nebo různoběžné, rovnici roviny ρ budeme moci snadno vyjádřit ze souřadnic bodu A nebo B a vektorů u a v. Budou-li přímky p a q mimoběžné, pak neexistuje žádná rovina, která by obě dvě obsahovala, kdyby byly totožné, tak by jich naopak bylo nekonečně mnoho.
• Ze souřadnic vektorů u a v je vidět, že přímky p a q nejsou rovnoběžné, mohou tedy být jen různoběžné nebo mimoběžné. Určíme jejich parametrické rovnice:
  
  

  p: x = -2 + t, y = 1 - t, z = -t; t ∈ .

  q: x = -3 - 3r, y = 5 + 2r, z = 1 + 3r; r ∈ .

• Abychom rozlišili, zda p × q nebo p q, musíme zjistit, kolik mají společných bodů. Hledáme takové body, které leží jak na přímce p, tak na přímce q. Řešíme soustavu tří rovnic o dvou neznámých:
  -2 + t = -3 - 3r,
  1 - t = 5 + 2r,
  -t = 1 + 3r.
• Pokud by tato soustava měla jedno řešení, přímky jsou různoběžné, nebude-li mít žádné, přímky jsou mimoběžné. Z poslední rovnice vyjádříme t = -3r - 1 a dosadíme do druhé rovnice:
  1 + 3r + 1 = 5 + 2r,
  r = 3.
• Dopočítáme vyjádřené t = -10 a do první rovnice dosadíme r = 3 a t = -10:
  -2 - 10 = -3 - 9,
  -12 = -12.
• To platí. Ukázali jsme, že soustava má právě jedno řešení r = 3, t = -10, tedy p × q. Protože jsou přímky p a q různoběžné, leží v jedné rovině. Tou je hledaná rovina ρ. Její parametrickou rovnici určíme ze souřadnic bodu A a vektorů u a v jako
  ρ:
  x = -2 + f - 3s,
  y = 1 - f + 2s,
  z = -r + 3f; f, s ∈ .

Jsou dány body A[-1; 0; 3], B[-1; 3; -2] a vektory u = (1; 2; 2) a v = (-2; 3; 1). Určete vzájemnou polohu přímek p(A, u) a q(B, v).

• Podíváme-li se na směrové vektory u a v zadaných přímek, vidíme, že vektor u není reálným násobkem vektoru v. To napovídá, že přímky p a q jsou buď různoběžné, nebo mimoběžné. Pokud jsou mimoběžné, nemají žádný společný bod, pokud jsou různoběžné, mají společný bod jeden.
  Hledáme společné body přímek p a q:
  

  p: x = -1 + t, y = 2t, z = 3 + 2t; t ∈ .

  q: x = -1 - 2s, y = 3 + 3s, z = -2 + s; s ∈ .

• Abychom určili společné body p a q, musíme vyřešit soustavu:
  -1 + t = -1 - 2s,
  2t = 3 + 3s,
  3 + 2t = -2 + s.
• Z první rovnice vyjádříme t = -2s. Dosadíme za t do třetí rovnice a vypočítáme s = 1. Dopočítáme t = - 2 a spočtené hodnoty parametrů s a t dosadíme do druhé rovnice:
  -4 = 3 + 3,
  -4 = 6.
• To neplatí pro žádné hodnoty parametrů s a t. Soustava nemá žádné řešení, a to znamená, že přímky p a q nemají žádný společný bod a mohou být buď rovnoběžné různé nebo mimoběžné. S přihlédnutím k úvaze na začátku řešení můžeme říci, že přímky p a q jsou mimoběžné.

Určete vzájemnou polohu přímky p(A, u) a roviny δ: 3x - y + 2z - 4 = 0, je-li A[2; -1; 2] a u = (2; 3; 2).

• Nejprve zkontrolujeme, zda je vektor u kolmý na normálový vektor roviny δ, vektor n. Kdyby kolmý byl, znamenalo by to, že přímka p je s rovinou δ rovnoběžná.
  
  

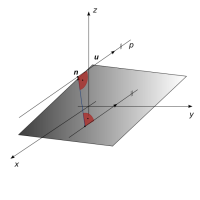
  Obrázek k úloze
  uv = 2⋅3 + 3⋅(-1) + 2⋅2 = 7.
• Vektor u není na v kolmý, to znamená, že přímka p je s rovinou δ různoběžná a má smysl hledat jejich průsečík. Obecnou rovnici roviny δ už známe, stačí najít parametrické vyjádření přímky p:
  p:
  x = 2 + 2t,
  y = -1 + 3t,
  z = 2 + 2t; t ∈ .
• Do obecné rovnice roviny δ dosadíme za x, y, z vztahy z parametrické rovnice přímky p:
  3(2 + 2t) - (-1 + 3t) + 2(2 + 2t) - 4 = 0,
  6 + 6t + 1 - 3t + 4 + 4t - 4 = 0,
  7t = -7,
  t = -1.
  To je hodnota parametru t odpovídající průsečíku roviny δ a přímky p. Odpovídá mu bod P[0; -4; 0].

Určete vzájemnou polohu přímky p(A, u) a roviny ρ: 3x - 2y - z + 2 = 0, je-li A[1; 2; 1] a u = (3; 3; 3).

• Nejprve zkontrolujeme, zda je vektor u kolmý na normálový vektor n = (3; -2; -1) roviny ρ:
  un = 3⋅3 + 3⋅(-2) + 3⋅(-1) = 0.
  To znamená, že přímka p je s rovinou ρ rovnoběžná různá nebo v ní leží. Pokud by byla rovnoběžná různá, nemohl by v rovině ρ ležet žádný její bod. Pokud by tam nějaký ležel, nutně by tam musela ležet celá přímka. Do obecné rovnice roviny ρ dosadíme souřadnice bodu A, abychom zjistili, zda A ∈ ρ.
• Získáme
  3 - 4 - 1 + 2 = 0,
  0 = 0.
  Bod A leží v rovině ρ, proto i přímka p leží v rovině ρ.

Určete vzájemnou polohu rovin ρ: 2x - 6y + z + 1 = 0 a φ: x + 3y + 2z - 4 = 0.

• Nejprve zjistíme, zda jsou roviny ρ a φ rovnoběžné, nebo různoběžné. Určíme normálový vektor roviny ρ, nρ = (2; -6; 1) a normálový vektor roviny φ, nφ = (1; 3; 2). Je vidět, že nρ není násobkem nφ a roviny ρ a φ jsou proto různoběžné. Má tedy smysl hledat jejich průsečnici . Řešíme soustavu dvou rovnic o třech neznámých:
  2x - 6y + z + 1 = 0,
  x + 3y + 2z - 4 = 0.
• Proměnnou y zvolíme za parametr, y = t a řešíme soustavu:
  2x - 6t + z + 1 = 0,
  x + 3t + 2z - 4 = 0.
• Z druhé rovnice vyjádříme x = 4 - 2z - 3t a dosadíme do rovnice první:
  2(4 - 2z - 3t) - 6t + z + 1 = 0,
  8 - 4z - 6t - 6t + z + 1 = 0,
  9 - 3z - 12t = 0,
  -3z = 12t - 9,
  z = 3 - 4t.
  Zpětně dopočítáme x = 4 - 2(3 - 4t) - 3t = -2 + 5t. Soustava má nekonečně mnoho řešení, které jsou závislé na různých hodnotách parametru t. Zvolený parametr t, je vlastně parametrem v rovnici průsečnice p rovin ρ a φ.
  p:
  x = -2 + 5t,
  y = t,
  z = 3 - 4t, t ∈ .

Najděte průsečnici p rovin ρ: x - 4y + 4z = 0 a φ: 2x - y + z - 7 = 0.

• Ze zadání plyne, že bychom měli hledat průsečnici rovin ρ a φ. Kontrolou jejich normálových vektorů se ujistíme, že zadání má smysl a že roviny jsou různoběžné:
  nρ = (1; -4; 4),
  nφ = (2; -1; 1).
• Je vidět, že nρ není násobkem nφ, roviny ρ a φ jsou různoběžné a má smysl hledat jejich průsečnici. Vyřešíme soustavu dvou rovnic o třech neznámých:
  x - 4y + 4z = 0,
  2x - y + z - 7 = 0.
• Proměnnou y zvolíme za parametr, y = t a vypočítáme soustavu:
  x - 4t + 4z = 0,                    (1)
  2x - t + z - 7 = 0.
• Od druhé rovnice odečteme dvojnásobek první a získáme:
  7t - 7z - 7 = 0,
  z = -1 + t.
• Po dosazení do (1) dopočítáme x = 4. Můžeme zapsat rovnici průsečnice p jako
  x = 4,
  y = t,
  z = -1 + t, t ∈ .

Spočítejte odchylku dvou přímek p(A; u) a q(B; v), je-li A[7; 7; 2], B[7; -8; 6], u = (-7; -1; 6) a v = (7; -8; -6).

• Dosadíme do vzorce a spočítáme cosφ
  \(\cosφ = \dfrac{|(-7) \cdot 7 + (-1) \cdot (-8) + 6 \cdot (-6)|}{\sqrt{(-7)^{2} + (-1)^{2} + 6^{2}} \cdot \sqrt{7^{2} + (-8)^{2} + (-6)^{2}}} = \dfrac{|-77|}{\sqrt{12814}} \approx 0,68\)
• φ ≈ 47°

Spočítejte odchylku přímky p(A; u) a roviny ρ: 6x + 2y + 1z - 4 = 0, je-li A[5; 5; 9], a u = (2; 3; -8).

• Využijeme toho, že odchylka φ přímky p a roviny ρ je rovna π/2 - α, kde α je odchylka kolmice na rovinu ρ a přímky p. Kolmice k rovině ρ má směrový vektor roven normálovému vektoru roviny ρ, který můžeme jednoduše určit z obecné rovnice této roviny.
• Dosadíme do vzorce a spočítáme cosα
  \(\cosα = \dfrac{|6 \cdot 2 + 2 \cdot 3 + 1 \cdot (-8)|}{\sqrt{6^{2} + 2^{2} + 1^{2}} \cdot \sqrt{2^{2} + 3^{2} + (-8)^{2}}} = \dfrac{|10|}{\sqrt{3157}} \approx 0,18\)
• α ≈ 80°.
• φ = π/2 - α ≈ 90° - 80° ≈ 10°.

Spočítejte odchylku rovin ρ: 4x - 4y - 6 = 0 a σ: 3x + 5y - 6z - 5 = 0.

• Normálové vektory rovin ρ i σ známe. Víme, že odchylka dvou rovin se rovná odchylce jejich normálových vektorů, můžeme tedy rovnou počítat jejich odchylku φ.
• Dosadíme do vzorce a spočítáme cosφ
  \(\cosφ = \dfrac{|4 \cdot 3 + (-4) \cdot 5 + 0 \cdot (-6)|}{\sqrt{4^{2} + (-4)^{2} + 0^{2}} \cdot \sqrt{3^{2} + 5^{2} + (-6)^{2}}} = \dfrac{|-8|}{\sqrt{2240}} \approx 0,17\)
• φ ≈ 80°.

Určete vzdálenost bodu B od přímky p(A, u), jestliže A[-2; 1; -2], B[3; 4; -3] a u = (2; 1; 1).

• Bodem B povedeme rovinu kolmou na přímku p. Ta přímku p protne v nějakém bodě Y. Vzdálenost |BY| je vzdálenost bodu B od přímky p.
• Normálový vektor roviny kolmé na přímku p je směrovým vektorem přímky p, tedy u = (2; 1; 1). Její obecná rovnice je 2x + y + z + e = 0. Koeficient e určíme po dosazení souřadnic bodu B do této rovnice:
  2⋅3 + 4 - 3 + e = 0,
  e = -7.
• Rovnice přímky p je:
  x = -2 + 2t,
  y = 1 + t,
  z = -2 + t; t ∈ .
• Hledáme bod Y, který je průsečíkem roviny 2x + y + z - 7 = 0 a přímky p:
  2(-2 + 2t) + (1 + t) + (- 2 + t) - 7 = 0,
  -4 + 4t + 2t - 8 = 0,
  6t = 12,
  t = 2.
• Bod Y leží na přímce p a jeho souřadnice odpovídají hodnotě parametru t = 2. Bod Y má souřadnice Y[2; 3; 0].
  \(d = |Bp| = |YB| = \sqrt{1^{2} + 1^{2} + (-3)^{2}} = \sqrt{11}.\)

Spočítejte vzdálenost bodu B[9; 4; -1] od roviny ρ: -3x + 3y + 6z + 8 = 0.

• Abychom spočetli vzdálenost bodu od roviny, stačí umět dosadit do vzorce pro její výpočet.
  \(d = \dfrac{|ap_{1} + bp_{2} + cp_{3} + e|}{\sqrt{a^{2} + b^{2} + c^{2}}}\).
• Dosadíme do vzorce a spočítáme d
  \(d = |Bρ| = \dfrac{|(-3) \cdot 9 + 3 \cdot 4 + 6 \cdot (-1) + 8|}{\sqrt{(-3)^{2} + 3^{2} + 6^{2}}} = \dfrac{|-13|}{\sqrt{54}} \approx 1,77\)
• d ≈ 1,77.

Vypočítejte vzdálenost rovin ρ: 2x - y + z - 5 = 0 a ψ: 4x - 2y + 2z - 13 = 0.

• Vzdálenost dvou rovin v prostoru se počítá podobně jako vzdálenost dvou přímek v rovině. Pokud jsou roviny různoběžné, je jejich vzdálenost rovna nule. Jsou-li rovnoběžné, je jejich vzdálenost rovna vzdálenosti libovolného bodu jedné z nich od té druhé. Roviny ρ a ψ jsou rovnoběžné, protože pro jejich normálové vektory, které získáme z obecné rovnice nρ = (2; -1; 1) a nψ = (4; -2; 2) platí nψ = 2nρ.
  
• Vzdálenost d rovin ρ a ψ je rovna vzdálenosti libovolného bodu roviny ρ od roviny ψ. Za bod roviny ρ zvolme například bod A[1; 2; 5]. Jeho vzdálenost od roviny ψ vypočítáme ze vzorce jako
  \(d = |Aψ| = \dfrac{|4\cdot 1 - 2\cdot 2 + 2\cdot 5 - 13|}{\sqrt{4^{2} + 2^{2} + 2^{2}}} = \dfrac{3}{\sqrt{24}} = \dfrac{3\sqrt{24}}{24} = \dfrac{\sqrt{24}}{8} \approx 0,61.\)

Vypočítejte vzdálenost přímek p(A, u), q(B, v), jestliže A[2; -1; -1], B[5; 1; 3], u = (2; 0; 1) a v = (4; 0; 2).

• Ze souřadnic směrových vektorů u a v je vidět, že přímky p a q jsou rovnoběžné. Platí, že v = 2u. Vzdálenost dvou rovnoběžných přímek p, q se rovná vzdálenosti libovolného bodu přímky p od přímky q. Bod, jehož vzdálenost od přímky q budeme počítat, může být například bod A.
• Bodem A povedeme rovinu ρ kolmou na přímku q. Ta přímku q protne v nějakém bodě Y. Vzdálenost |AY| je vzdálenost bodu A od přímky q.
• Normálový vektor roviny kolmé na přímku q je směrovým vektorem přímky q, tedy vρ = v = (4; 0; 2). Její obecná rovnice je 4x + 2z + d = 0. Koeficient d určíme po dosazení souřadnic bodu A do této rovnice:
  4⋅2 + 2⋅(-1) + d = 0,
  d = -6.
• Rovnice přímky q je:
  x = 5 + 4t,
  y = 1,
  z = 3 + 2t; t ∈ .
• Hledáme bod Y, který je průsečíkem roviny ρ: 4x + 2z - 6 = 0 a přímky q:
  4(5 + 4t) + 2(3 + 2t) - 6 = 0,
  20 + 16t + 6 + 4t - 6 = 0,
  20t + 20 = 0,
  t = -1.
• Bod Y leží na přímce q a jeho souřadnice odpovídají hodnotě parametru t = -1. Bod Y má souřadnice Y[1; 1; 1]. Vzdálenost d přímek p a q je rovna vzdálenosti bodů Y a A:
  \(|d| = |pq| = |YA| = \sqrt{1^{2} + (-2)^{2} + (-2)^{2}} = \sqrt{9} = 3\).

Vypočítejte vzdálenost přímek p(A, u), q(B, v), je-li A[2; 2; 0], B[4; -1; 3], u = (-2; 3; 1) a v = (-1; 2; 1).

• Přímky p a q nejsou rovnoběžné, to vidíme ze souřadnic vektorů u a v, protože u není reálným násobkem vektoru v. Přímky p a q mohou být různoběžné, nebo mimoběžné. Zjistíme to v závislosti na tom, kolik mají společných bodů nebo s použitím následující úvahy:
  Rovina ρ určená bodem A a vektory u a v může nebo nemusí obsahovat bod B. Pokud bod B leží v této rovině, přímky p a q jsou různoběžné. Není-li tomu tak, jsou mimoběžné. Rovina určená bodem A a vektory u a v má rovnici:
  x = 2 - 2t - s,
  y = 2 + 3t + 2s,
  z = 0 + t + s; t, s ∈ .
• Aby bod B ležel v rovině ρ, muselo by platit
  4 = 2 - 2t - s,
  -1 = 2 + 3t + 2s,
  3 = t + s.
• Přičteme první rovnici k poslední a vyjádříme t = -5. Ze třetí rovnice dopočítáme s = 8. Dosadíme t = -5, s = 8 do druhé rovnice:
  -1 = 2 - 15 + 16,
  -1 = 3.
  Soustava nemá řešení, z toho plyne, že bod B v rovině určené bodem A a vektory u a v neleží. Přímky p a q jsou proto mimoběžné a jejich vzdálenost je nenulová.
• Vzdálenost dvou mimoběžných přímek je rovna minimální vzdálenosti kterýchkoliv dvou jejich bodů. Dvojice bodů, která určuje tuto vzdálenost, je právě jedna. Jsou to body X[x1; x2; x3] na přímce p a Y[y1; y2; y3] na přímce q takové, že přímka XY je kolmá jak na přímku p, tak na přímku q. Úsečka XY se nazývá příčka mimoběžek. Ve své úvaze můžeme jít ješte dále. Najdeme-li rovinu ρ, která obsahuje přímku p a jejímž normálovým vektorem je vektor XY, zjistíme, že přímka q je s ní rovnoběžná. Vzdálenost přímky q od roviny ρ je rovna délce jejich příčky.
  
• Směrový vektor w příčky XY je kolmý na vektory u i v. Takový vektor získáme jako u × v:
  w = u × v = (1; 1; -1).
• Rovina ρ s normálovým vektorem w má rovnici
  x + y - z + d = 0. Má-li rovina ρ obsahovat přímku p, musí kromě u obsahovat i bod A. Do rovnice ρ dosadíme souřadnice bodu A a dopočítáme koeficient d:
  2 + 2 + d = 0,
  d = -4.
• Hledáme vzdálenost d bodu B od roviny ρ: x + y - z - 4 = 0:
  \(d = |Bρ| = \dfrac{|4 - 1 - 3 - 4|}{\sqrt{1^{2} + 1^{2} + (-1)^{2}}} = \dfrac{4}{\sqrt{3}} = \dfrac{4\sqrt{3}}{3}\).