Odchylka přímek
V posledních dvou kapitolách si rozšíříme paletu úloh, které umíme řešit. V této kapitole si ukážeme, jak vypočítat odchylku přímek. V poslední kapitole se naučíme počítat vzdálenost bodu od přímky a vzdálenost dvou přímek.
Odchylka přímek p(P, u), q(Q, v) je číslo φ ∈ <0, π/2>, pro které platí: \(\cosφ = \dfrac{|uv|}{|u|\cdot|v|}\).
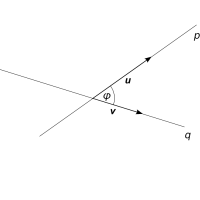
Jsou dány přímky p a q. Přímka p je určena body A = [2; 0] a B = [1; 6] a přímka q rovnicí 2x - y + 1 = 0. Určete jejich odchylku.
- Směrový vektor up přímky p určíme jako vektor
AB = (-1; 6). Z rovnice přímky q nejdříve vyjádříme její normálový vektor, který převedeme na vektor směrový: nq = (2; -1) a uq je tedy (1; 2).
\(\cosφ = \dfrac{|-1 + 12|} {\sqrt{5} \cdot \sqrt{37}} \approx 0.8087\). - Nelekejte se získaného výsledku, jen málokdy se totiž stane, aby řešením podobné úlohy byla některá z tzv. tabulkových hodnot. Využijte kalkulačky a výsledek zaokrouhlete na stupně.
- φ ≈ cos-1(0.8087) ≈ 36°.
K výpočtu odchylky dvou přímek, které jsou zadány svými obecnými rovnicemi můžeme využít i jejich normálové vektory. Z obr. 3.11 plyne, že odchylka přímek p, q je stejná jako odchylka přímek r, s, jejichž směrovými vektory jsou normálové vektory přímek p a q.
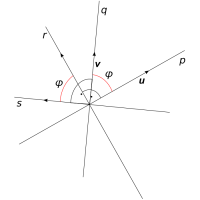
Vypočítejte odchylku přímek p: -1x + 2y - 7 = 0 a q: 9x + 5 = 0. Výsledek zaokrouhlete na stupně.
