Basic information
Warning: This page concerned the lectures given in summer semester 2019/20. Please consult the homepage for information about current lectures.
Starting from March 11, 2020, all the lectures are canceled because of the coronavirus epidemy. According to the decision of the Rector and the Dean, this should be interpreted as that the course is still running using other means of communication. Currently, the course is running as follows:
- I will stream lectures at usual times using Zoom. The lectures are recorded and stored here, so you can access them later.
- The homework assignments are also supposed to be delivered within deadlines (preferably via e-mail in PDF, pictures and scans of handwritten solutions are perfectly acceptable when readable).
- You can contact me or my colleague Jakub Kopřiva via e-mail and we can arrange on-line consultations on individual basis.
The aim of the course is to give an introduction to representation theory of finite dimensional algebras and illustrate the lectured concepts on examples. The contents of the course and other basic information are available in the Student Information System.
The schedule (to be found also in the Student Information System):
- Thursday, 10.40am-12.10pm and
- Thursday, 2.00pm-3.30pm
in the seminar room of the Department of Algebra (pre-coronavirus times) or Zoom. The problem sessions (with Jakub Kopřiva) take place once in two weeks from 2.00pm to 3.30pm.
Exam
The exam will be oral. A distance form of the exam using a video call will be possible (the rules and recommendations for that option are still under construction, however). Please contact me to agree on the date and time of your exam in due time.
Credit
The credit will be granted for solved exercise problems. There will be three sets of the problems which will appear here. Requested are at least 50 % of successfully solved problems handed in within the deadlines.
- Problem set #1 (hand in by April 9):
- Exercises 7, 13, 15 and 17 from Section II.4 Exercises (p. 65-68) in the monograph by Assem, Simson, Skowroński.
- Problem set #2 (hand in by May 7):
-
The following exercises from Section III.4 (p. 93-96) in the monograph by Assem, Simson, Skowroński:
- Exercise 4(a), (c), (g), (h),
- Exercise 5,
- Exercise 10,
- A variant of Exercise 10: Keep the quiver Q, but change the ideal I to just ⟨βα⟩. What is the global dimension of A = KQ/I now?
- Problem set #3:
-
- Find a root of the Dynkin diagram E6 which has number 3 in one of its components. Choose an orientation of the diagram and describe the corresponding indecomposable representation of the resulting quiver.
-
Let Q be the 4-subspace quiver, i.e.
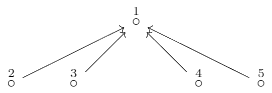
Find the four lowest possible dimensions of preprojective indecomposable representations of Q and for each dimension exhibit one such representation.
What has been lectured
A brief overview of what has been taught in individual lectures, including references to the literature, can be found below.
- February 20, 2020
- Quivers and their representations in the category of vectors spaces, some motivating problems (e.g. configurations of subspaces of a given space). Additive and K-linear categories. Equivalence between the categories of representations of a quiver and module categories over the corresponding path algebras ([ASS], Ch. I, Sec. II.1, Sec. III.1).
- February 27, 2020
- The category of representations of Q bound by a set relations is equivalent to modules over the corresponding quotient of KQ. Admissible ideals of path algebras. The Jacobson radical of a ring. If A=KQ/I with Q finite and I admissible, then the radical is generated by the arrows of Q ([ASS], Ch. I, Sec. II.2, Sec. III.1). Exercises: see the exercise sheet #1.
- March 5, 2020
- The Nakayama lemma. Idempotent elements and direct sum decomposition of a ring to right ideals, finite dimensional algebras have complete sets of primitive orthogonal idempotents. Central idempotents, connected rings, an interpretation for algebras of the form KQ/I for an admissible ideal I. Local rings and a characterization of local finite dimensional algebras. Idempotents in endomorphism rings of modules and the relation to direct sum decomposition. The Krull-Schmidt theorem on the uniqueness of direct sum decomposition ([ASS], Sec. I.4, Sec. II.1 - II.2).
- March 12, 2020
- Self-study: The Krull-Schmidt theorem (completing the proof), the Jacobson radical of a module, projective covers ([ASS], Sec. I.3 - I.5). Exercises: see the exercise sheet #2.
- March 19, 2020
- Self-study: Duality between the categories of left and right finite dimensional modules, the socle of a module, injective modules and injective envelopes. Basic algebras, Morita equivalence (= equivalence of module categories for two algebras), the quiver of a finite dimensional algebra ([ASS], Sec. I.2.9 on p. 12, end of p. 14 in Sec. I.3, the rest of I.5, Sec. I.6, p. 59-63 in Sec. II.3, and Sec. III.2 up to Examples 2.7).
- March 26, 2020
- Streamed lecture: the Jacobson radical of a module, projective covers, the vector space duality between left and right modules, injective modules (recorded lecture, handwritten notes, [ASS], Sec I.2.9, I.3, I.5, III.2). Exercises: see the exercise sheet #3.
- April 2, 2020
- Streamed lectures: The socle of a module and the existence and the structure of injective envelopes. Basic algebras, Morita equivalence, the quiver of a (suitable) finite dimensional algebra. Gabriel's theorem on that every finite dimensional algebra over an algebraically closed field is Morita equivalent to a path algebra modulo an admissible ideal. Crash course on the Ext functors (recorded lectures, presentation for lecture 1, presentation for lecture 2, [ASS], Sec. I.3, I.6, II.3).
- April 9, 2020
- Streamed lecture: Homological dimensions, hereditary rings, finite dimensional hereditary algebras over an algebraically closed field are Morita equivalent to path algebras without relations (recorded lecture, presentation for the lecture, whiteboards from the lecture, [ASS], Sec. VII.1). Exercises: see the exercise sheet #4.
- April 16, 2020
- Streamed lectures: The Grothendieck group of a path algebra and dimension vectors, the Euler bilinear form, symmetric bilinear and quadratic forms associated with finite graphs. The classification of connected graphs with positive definite quadratic form (Dynkin diagrams) and positive semi-definite quadratic form (Euclidean diagrams). Roots corresponding to Dynkin and Euclidean diagrams. (recorded lectures, presentation for lecture 1, whiteboards from lecture 1, presentation for lecture 2, whiteboards from lecture 2, [Kra], Sec. 3.2, 4.1-4.3, [ASS], Sec. III.3).
- April 23, 2020
- Streamed lecture: Roots and reflections in Zn, admissible ordering of vertices of a quiver, the Coxeter transformation. Reflection functors and their properties, the induced bijections between indecomposable representations of Q and σiQ with the exception of the simples at vertex i (recorded lectures, presentation for the lecture, [Kra], Sec. 3.1-3.3, 4.3, 4.4). Exercises: see the exercise sheet #5.
- April 30, 2020
- Streamed lectures: Reflection functors (finishing a proof), Coxeter functors and the Coxeter transformation revisited. Preprojective and preinjective representations. Gabriel's theorem on finite representation type, a bijection between the isoclasses of indecomposable representations and the positive roots in the Dynkin case, examples. The defect of a representation of a Euclidean quiver and how it determines the type of the representation (preprojective/preinjective/regular) (recorded lectures, presentation for lecture 1, presentation for lecture 2, whiteboards from lecture 2, [Kra], Sec. 3.3 - 3.5, 4.4, 5.1 - 5.3).
- May 7, 2020
- Streamed lecture: Regular representations and direction of morphisms. The classification of indecomposable representations of the Kronecker quiver (recorded lectures, presentation for the lecture, whiteboards from the lecture, [Kra], Sec. 5.3, 9.1 - 9.3). Exercises: see the exercise sheet #6.
- May 21, 2020
- Streamed lectures: The radical of a module category, the Harada-Sai lemma. Morphisms between preprojective representations of a finite acyclic quiver in terms of generating morphisms (=specific irreducible morphisms induced by arrows of the quiver) and relations, coming all from certain short exact sequences (recorded lectures, presentation for lecture 1, whiteboards from lecture 1, presentation for lecture 2, whiteboards from lecture 2, [Kra], Sec. 6.1 - 6.3, 7.1 - 7.5).
- May 28, 2020
- Exercises: see the exercise sheet #7.
Literature
The lectured material will be mostly based on the following sources:
| [ASS] | I. Assem, D. Simson, A. Skowroński, Elements of the representation theory of associative algebras, Vol. 1, Cambridge University Press, 2006. |
| [Kra] | H. Krause, Representations of quivers via reflection functors, arXiv:0804.1428. [Full text in PDF] |
The course roughly covers the first three chapters of [ASS] (with a short venture to Section VII.1 because of hereditary algebras) and Sections 3 to 5 in [Kra] (possibly with a brief account on Section 9 about the Kronecker quiver as well).
Several other monographs on the topic of representation theory of finite dimensional algebras appeared recently. There is, however, also an older one which is certainly worth mentioning:
| [ARS] | M. Auslander, I. Reiten, S. Smalø, Representation theory of Artin algebras, Cambridge University Press, 1997. |
Other links
- Homepage of the course from 2018/19.
- Computations with path algebras are implemented in the QPA package of the computer algebra system GAP. See also the webpage of Øyvind Solberg, who maintains the package.