\begin{align} \end{align}


2.3 Odmocniny z reálného čísla

V první kapitole jsme si připomněli pojem druhá odmocnina z reálného čísla. Nyní tyto znalosti rozšíříme definováním \(n\)-té odmocniny z reálného čísla, \(n \in \mathbb N\).

Definice

Pro libovolné \(n \in \mathbb N\) definujeme \(n\)-tou odmocninu z nezáporného reálného čísla \(a\) jako nezáporné reálné číslo \(b\), pro které platí \(b^n = a\). Značíme \(\displaystyle b = \sqrt[\large n \,]{a \;}\).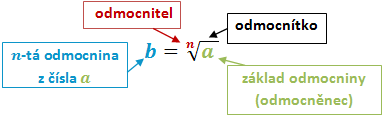
Číslo \(a\) označujeme jako základ odmocniny (odmocněnec), číslo \(n\) nazýváme odmocnitel a symbol \(\sqrt{\; \; \;}\) je odmocnítko.
odmocnina

Říkáme, že "odmocněním čísla \(a\) dostaneme číslo \(b\)".

V souladu s dříve zavedeným značením budeme pro druhou odmocninu užívat zkrácený zápis \(b = \sqrt{a}\) namísto zápisu \(\displaystyle b = \sqrt[\large 2 \,]{a \;}\).

Poznámka

Z definice vyplývá, že \(n\)-tá odmocnina je definována pouze z nezáporného čísla a zároveň že \(n\)-tá odmocnina je vždy nezáporná.

Příklad 2.8

Odmocni:
a) \(\displaystyle \sqrt[\large 3 \,]{27 \;}\) b) \(\displaystyle \sqrt[\large 4 \,]{16 \;}\) c) \(\displaystyle \sqrt[\large 3 \,]{\frac {1} {125} \;}\) d) \(\displaystyle \sqrt[\large 4 \,]{0,000\,1 \;}\)

Řešení

a) \(\displaystyle \sqrt[\large 3 \,]{27 \;} = 3\), jelikož \(3^3 = 27\)

b) \(\displaystyle \sqrt[\large 4 \,]{16 \;} = 2\), jelikož \(2^4 = 16\)

c) \(\displaystyle \sqrt[\large 3 \,]{\frac {1} {125} \;} = \frac {1} {5}\), jelikož \(\displaystyle \left(\frac {1} {5}\right)^3 = \frac {1} {125}\)

d) \(\displaystyle \sqrt[\large 4 \,]{0,000\,1 \;} = 0,1\), jelikož \((0,1)^4 = 0,000\,1\)


Pro počítání s odmocninami platí následující pravidla:

Pro všechna nezáporná reálná čísla \(a\), \(b\) a pro všechna přirozená čísla \(m\), \(n\) platí:
1. \(\displaystyle \sqrt[\large n \,]{a \;} \cdot \sqrt[\large n \,]{b \;} = \sqrt[\large n \,]{ab \;}\) 2. \(\displaystyle \sqrt[\large n \,]{a_1 \;} \cdot \dots \cdot \sqrt[\large n \,]{a_m \;} = \sqrt[\large n \,]{a_1 \cdot \dots \cdot a_m \;}\)

3. \(\displaystyle \frac {\sqrt[\large n \,]{a \;}} {\sqrt[\large n \,]{b \;}} = \sqrt[\large n \,]{\frac{\; a \;} {\; b \;} \;}\) , pro \(b \neq 0\)

(Tvrzení 2 představuje zobecnění tvrzení 1.)

Příklad 2.9

Odmocni:
a) \(\displaystyle \frac {\sqrt[\large 5]{96\;}} {\sqrt[\large 5 \;]{3\;} \;}\) b) \(\displaystyle \sqrt{36\pi^4 \;}\) c) \(\displaystyle \sqrt[\large 3 \;]{10 \;} \cdot \sqrt[\large 3 \;]{25 \;} \cdot \sqrt[\large 3 \;]{4\;}\) d) \(\displaystyle \sqrt[\large 3 \;]{\frac {54}{125}}\)

Řešení

a) \(\displaystyle \frac {\sqrt[\large 5 \;]{96 \;}} {\sqrt[\large 5 \;]{3 \;}} = \sqrt[\large 5 \;]{\frac {96} {3} \;} = \sqrt[\large 5 \;]{32 \;} = 2\)

b) \(\displaystyle \sqrt{36\pi^4 \;} = \sqrt{36 \;} \cdot \sqrt {\pi^4 \;} = 6\pi^2\)

c) \(\displaystyle \sqrt[\large 3 \;]{10 \;} \cdot \sqrt[\large 3 \;]{25 \;} \cdot \sqrt[\large 3 \;]{4 \;} = \sqrt[\large 3 \;]{10 \cdot 25 \cdot 4 \;} = \sqrt[\large 3 \;]{1 \, 000 \;} = 10\)

d) \(\displaystyle \sqrt[\large 3 \;]{\frac {54}{125} \;} = \frac {\sqrt[\large 3 \;]{54 \;}} {\sqrt[\large 3 \;]{125 \;}} = \frac {\sqrt[\large 3 \;]{27 \;} \cdot \sqrt[\large 3 \;]{2 \;}} {5} = \frac {3 \cdot \sqrt[\large 3 \;]{2 \;}} {5}\)

V příkladu 2.9 d) jsme provedli částečné odmocnění.


Pro všechna přirozená čísla \(n\), pro všechna celá čísla \(z\) a pro všechna kladná reálná čísla \(a\) platí:
1. \(\displaystyle \left(\, \sqrt[\Large n \,]{\large a \;}\right)^{\large z} = \sqrt[\large n \,]{\large a^{\large \, z} \;}\) 2. \(\displaystyle \left(\, \sqrt[\Large n \,]{\large a \;}\right)^{\large n} = \sqrt[\Large n \,]{\large a^{\large \, n} \;} = \large a\)

(Tvrzení 2 je speciální případ tvrzení 1 pro \(z = n\).)

Pro všechna přirozená čísla \(m\), \(n\), \(p\) a pro všechna nezáporná reálná čísla \(a\) platí:
1. \(\displaystyle \sqrt[\LARGE m \,]{\sqrt[\LARGE n \,]{\large a \;} \;} = \sqrt[\LARGE n \,]{\sqrt[\LARGE m \,]{\large a \;} \;} = \sqrt[\LARGE mn \,]{\large a \;}\) 2. \(\displaystyle \sqrt[\LARGE np \,]{\large a^{\large mp} \;} = \sqrt[\LARGE n \,]{\large a^{\large m} \;}\)

Příklad 2.10

Zjednoduš:
a) \(\displaystyle \left(\sqrt[\large 7 \,]{\frac {\, 1 \,} {2}\;}\right)^7\) b) \(\displaystyle \sqrt[\large 6 \,]{4^2 \;} \cdot \sqrt[\large 6 \,]{4^4 \;}\) c) \(\displaystyle \sqrt[\large 3 \,]{\sqrt{2 \;} \;}\) d) \(\displaystyle \sqrt[\large 6 \,]{4^9 \;}\)

Řešení

a) \(\displaystyle \left(\sqrt[\large 7 \,]{\frac {\, 1 \,} {2} \;}\right)^7 = \sqrt[\large 7 \,]{\left(\frac {\, 1 \,} {2}\right)^7 \;} = \frac {\, 1 \,} {2}\)

b) \(\displaystyle \sqrt[\large 6 \,]{4^2 \;} \cdot \sqrt[\large 6 \,]{4^4 \;} = \sqrt[\large 6 \,]{4^2 \cdot 4^4 \;} = \sqrt[\large 6 \,]{4^6 \;} = 4\)

c) \(\displaystyle \sqrt[\large 3 \,]{\sqrt{2 \;} \;} = \sqrt{\sqrt[\large 3 \,]{2 \;} \;} = \sqrt[\large 3 \cdot 2 \,]{2 \;} = \sqrt[\large 6 \,]{2 \;}\)

d) \(\displaystyle \sqrt[\large 6 \,]{4^9 \;} = \sqrt[\large 3 \cdot 2]{4^{3 \cdot 3} \;} = \sqrt[\large 2 \,]{4^3 \;} = \sqrt{64 \;} = 8\)


Příklad 2.11

Vyjádři ve tvaru jediné odmocniny za předpokladu, že \(a > 0\):
a) \(\displaystyle \sqrt[\large 5 \,]{a \;} \cdot \sqrt{a^3 \;}\) b) \(\displaystyle \sqrt[\large 4 \,]{a \cdot \sqrt[\large 3 \,]{a \;} \;}\)

Řešení

a) Každou odmocninu zapíšeme ve tvaru odmocniny, kde odmocnitel je \(10\) (což je nejmenší společný násobek čísel \(2\) a \(5\)).
\(\displaystyle \sqrt[\large 5 \,]{a \;} \cdot \sqrt{a^3 \;} = \sqrt[\large 5 \,\cdot \,2 \,]{a^2 \;} \cdot \sqrt[\large 2 \, \cdot \, 5 \,]{\left(a^3\right)^5 \;} = \sqrt[\large 10 \,]{a^2 \;} \cdot \sqrt[\large 10 \,]{\left(a^3\right)^5 \;} = \sqrt[\large 10 \,]{a^2 \cdot a^{15} \;} = \sqrt[\large 10 \,]{a^{17} \;}\)

b) \(\displaystyle \sqrt[\large 4 \,]{a \cdot \sqrt[\large 3 \,]{a \;} \;} = \sqrt[\large 4 \,]{\sqrt[\large 3]{a^3 \;} \cdot \sqrt[\large 3 \,]{a \;}\;} = \sqrt[\large 4 \,]{\sqrt[\large 3 \,]{a^3 \cdot a \;} \;} = \sqrt[\large 4 \,]{\sqrt[\large 3 \,]{a^4 \;} \;} = \sqrt[\large 4 \, \cdot \, 3 \,]{a^4 \;} = \sqrt[\large 3 \,]{a \;}\)


Poznámka

Podle definice \(n\)-té odmocniny z nezáporného reálného čísla má smysl také zápis \(\sqrt[\large 1 \,]{a^m}\) ,
přičemž \(\sqrt[\large 1 \,]{a^m} = a^m\).

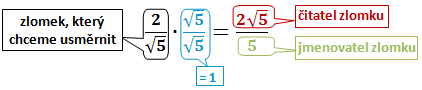
Usměrňování zlomku

V případě, že se ve jmenovateli zlomku vyskytuje odmocnina, upravujeme obvykle zlomek tak, aby ve jmenovateli žádné odmocniny nebyly. Tento postup se nazývá usměrňování zlomku. Zlomek usměrníme vhodným rozšířením, tedy vynásobením čitatele i jmenovatele zlomku stejným nenulovým číslem (tím se hodnota původního zlomku nezmění). Při usměrňování zlomku je někdy výhodné využít vzorec pro rozdíl druhých mocnin.

odmocnina

Příklad 2.12

Usměrni zlomky:
a) \(\displaystyle \frac {3} {4 \sqrt{3 \;}}\) b) \(\displaystyle \frac {1}{\sqrt[\large 3 \,]{7 \;}}\) c) \(\displaystyle \frac {3} {1 - \sqrt{2 \;}}\) d) \(\displaystyle \frac {4} {\sqrt{5 \;} + \sqrt {3 \;}}\)

Řešení

a) \(\displaystyle \frac {3} {4 \sqrt{3 \;}} \cdot \frac {\sqrt{3 \;}} {\sqrt{3 \;}} = \frac {3\sqrt{3 \;}} {4 \cdot 3} = \frac {\sqrt{3 \;}} {4}\)

b) \(\displaystyle \frac {1}{\sqrt[\large 3 \,]{7 \;}} \cdot \frac {\sqrt[\large 3 \,]{7 \;} \cdot \sqrt[\large 3 \,]{7 \;}} {\sqrt[\large 3 \,]{7 \;} \cdot \sqrt[\large 3 \,]{7 \;}} = \frac {\sqrt[\large 3 \,]{49}} {7}\)

c) \(\displaystyle \frac {3} {1 - \sqrt{2 \;}} \cdot \frac {1 + \sqrt{2 \;}} {1 + \sqrt{2 \;}} = \frac {3\left(1 + \sqrt{2} \right)} {1^2 - \left(\sqrt{2}\right)^2} = \frac {3 \left(1 + \sqrt{2} \right)} {1 - 2} = - \, 3\left(1 + \sqrt{2} \right)\)

Využili jsme vzorec \((a - b)(a + b) = a^2 - b^2\), kde \(a = 1\), \(b = \sqrt{2}\).

d) \(\displaystyle \frac {4} {\sqrt{5} + \sqrt {3}} \cdot \frac {\sqrt{5} - \sqrt{3}} {\sqrt{5} - \sqrt{3}} = \frac {4 \left(\sqrt{5} - \sqrt{3} \right)} {\left(\sqrt{5 \;} \right)^2 - \left(\sqrt{3 \;} \right)^2} = \frac {4 \left(\sqrt{5} - \sqrt{3} \right)} {5 - 3} = \frac {4 \left(\sqrt{5} - \sqrt{3} \right)} {2} = \)

\(\displaystyle = 2 \left(\sqrt{5} - \sqrt{3} \right)\)

Využili jsme vzorec \((a + b)(a - b) = a^2 - b^2\), kde \(a = \sqrt{5}\), \(b = \sqrt{3}\).



Cvičení k této části.