4.3 Rozšiřování lomených výrazů, jejich součet a rozdíl
V této části se budeme věnovat sčítání a odčítání lomených výrazu. Abychom tyto operace zvládli, potřebujeme umět lomené výrazy rozšiřovat.
Rozšiřování lomených výrazů
lze rozšiřování lomeného výrazu vyjádřit jako:
\(\displaystyle \frac {V_1} {V_2} = \frac {V_1 \cdot V_3} {V_2 \cdot V_3}\)

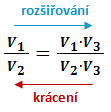
Následující schéma znázorňuje vztah mezi rozšiřováním a krácením lomených výrazů:
Příklad 4.8
uvedenému v závorce:
| a) \(\displaystyle \frac {a} {a - 4}\) \(\displaystyle \left[ \frac {?} {a^2 - 4a}\right]\) | b) \(\displaystyle \frac {a + 2} {3 - a}\) \(\displaystyle \left[\frac {?} {a - 3}\right]\) | c) \(\displaystyle \frac {a + 4} {4 - a}\) \(\displaystyle \left[\frac {?} {16 - a^2}\right]\) |
Řešení
a) Lomený výraz rozšíříme výrazem \(a\).
\(\; \; \displaystyle \frac {a \cdot a} {(a - 4) \cdot a} = \frac {a^2} {a^2 - 4a}\)
Rozšířený lomený výraz má smysl za podmínky, že \(a \in \mathbb R - \{0; 4\}\).
b) Lomený výraz rozšíříme výrazem \(-1\).
\(\; \; \displaystyle \frac {(a + 2) \cdot (-1)} {(3 - a) \cdot (-1)} = \frac {-a - 2} {a - 3}\)
Rozšířený lomený výraz má smysl za podmínky, že \(a \in \mathbb R - \{3\}\).
c) Lomený výraz rozšíříme výrazem \(4 + a\).
\(\; \; \displaystyle \frac {(a + 4)(4 + a)} {(4 - a)(4 + a)} = \frac {(a + 4)^2} {16 - a^2}\)
Rozšířený lomený výraz má smysl za podmínky, že \(a \in \mathbb R - \{\pm 4\}\).
Příklad 4.9
a) \(\displaystyle \frac {2} {b^3} \; \;\) a \(\displaystyle \; \; \frac {3} {b(b + 1)}\)
Řešení
a) První lomený výraz rozšíříme jmenovatelem druhého výrazu, druhý lomený výraz jmenovatelem prvního výrazu
\(\displaystyle \frac {2 \cdot b(b + 1)} {b^3 \cdot b(b + 1)} = \frac {2b(b + 1)} {b^4(b + 1)} \; \;\) a \(\displaystyle \; \; \frac {3 \cdot b^3} {b(b + 1) \cdot b^3} = \frac {3b^3} {b^4(b + 1)}\) .
Získali jsme lomené výrazy se stejným výrazem ve jmenovateli. Vidíme ovšem, že oba nově vzniklé lomené výrazy lze krátit výrazem \(b\), čímž dostaneme
\(\displaystyle \frac {2(b + 1)} {b^3(b + 1)} \; \;\) a \(\displaystyle \; \; \frac {3b^2} {b^3(b + 1)}\) ,
tudíž opět dva lomené výrazy, které odpovídají zadání.
Které řešení tedy platí? Správné jsou obě varianty, ale preferujeme druhé vyjádření
(mocnina \(b^3\) je nižší než \(b^4\)).
Podmínky: \(b \in \mathbb R - \{-\,1; 0\}\)
V předchozím příkladě jsme vlastně ve jmenovateli hledali společný násobek mnohočlenů - takový výraz, který lze beze zbytku dělit původními mnohočleny. Postup, jak ho určit, ilustruje také následující příklad.
Příklad 4.10
| a) \(4a^2(b + 1)^2 \; \;\) a \(\; \; 6a^4(b + 1)\) | b) \(20(a - 2)^2 \; \;\) a \(\; \; 15(a^2 - 4)\) |
Řešení
a) Oba mnohočleny rozložíme na součin.
\(4a^2(b + 1)^2 = 2 \cdot 2 \cdot a \cdot a \cdot (b + 1) \cdot (b + 1)\)
\(6a^4(b + 1) = 2 \cdot 3 \cdot a \cdot a \cdot a \cdot a \cdot (b + 1)\)
Jako společný násobek označíme součin, jehož činitelé jsou činiteli alespoň v jednom rozkladu výrazů,
přičemž mocnitelé u těchto činitelů korespondují s nejvyšším počtem jejich výskytů v těchto rozkladech,
tj. \(2^2 \cdot 3^1 \cdot a^4 \cdot (b + 1)^2 = 12a^4(b + 1)^2\).
Společným násobkem zadaných mnohočlenů je výraz \(12a^4(b + 1)^2\).
b) Oba mnohočleny rozložíme na součin.
\(20(a - 2)^2 = 2 \cdot 2 \cdot 5 \cdot (a - 2) \cdot (a - 2)\)
\(15(a^2 - 4) = 3 \cdot 5 \cdot (a + 2) \cdot (a - 2)\)
Společným násobkem zadaných mnohočlenů je výraz \(2^2 \cdot 3^1 \cdot 5^1 \cdot (a - 2)^2 \cdot (a + 2)^1 =
60(a + 2)(a - 2)^2\).
Sčítání lomených výrazů
platí pro součet lomených výrazů:
\(\displaystyle \frac {V_1} {V_2} + \frac {V_3} {V_4} = \frac {V_1 \cdot V_4 + V_3 \cdot V_2} {V_2 \cdot V_4}\)
Při sčítání lomených výrazů používáme převod na společného jmenovatele, obdobně jako u sčítání zlomků. Často je výhodnější nechat jmenovatele v průběhu řešení ve tvaru součinu než jej roznásobovat.
Příklad 4.11
| a) \(\displaystyle \frac {x - 9} {3} + \frac {x + 3} {x}\) | b) \(\displaystyle \frac {3 - x} {x^2 - 9} + \frac {1} {x^2 + 3x} + \frac {1} {x}\) |
Řešení
a) Společný jmenovatel je \(3 \cdot x\), proto:
\(\displaystyle \frac {x - 9} {3} + \frac {x + 3} {x} =
\frac {(x - 9) \cdot x + (x + 3) \cdot 3} {3 \cdot x} =
\frac {x^2 - 9x + 3x + 9} {3x} = \frac {x^2 - 6x + 9} {3x} = \frac {(x - 3)^2} {3x}\)
Výpočet má smysl za podmínky, že \(x \in \mathbb R - \{0\}\).
b) Společný jmenovatel je \((x + 3)(x - 3)x\), proto:
\(\displaystyle \frac {3 - x} {x^2 - 9} + \frac {1} {x^2 + 3x} + \frac {1} {x} =
\frac {3 - x} {(x + 3)(x - 3)} + \frac {1} {x(x + 3)} + \frac {1} {x} = \)
\(\displaystyle = \frac {(3 - x) \cdot x + 1 \cdot (x - 3) + 1 \cdot (x + 3)(x - 3)} {(x + 3)(x - 3)x} =
\frac {3x - x^2 + x - 3 + x^2 - 9} {x(x + 3)(x - 3)} =
\frac {4x - 12} {x(x + 3)(x - 3)} = \)
\(\displaystyle = \frac {4(x - 3)} {x(x + 3)(x - 3)} =
\frac {4} {x(x + 3)}\)
Výpočet má smysl za podmínky, že \(x \in \mathbb R - \{-\,3; 0; 3\}\).
Odčítání lomených výrazů
Pro odčítání lomených výrazů nepotřebujeme znát žádné nové pravidlo, stačí pouze využít tvrzení pro součet lomených výrazů a výrazy vhodně upravit.

platí pro rozdíl lomených výrazů:
\(\displaystyle \frac {V_1} {V_2} - \frac {V_3} {V_4} = \frac {V_1 \cdot V_4 - V_3 \cdot V_2} {V_2 \cdot V_4}\)
Pro připomenutí ještě zdůrazněme, že znaménko "\(-\)" před lomeným výrazem se vztahuje k celému výrazu, což ilustruje následující příklad:
\(\displaystyle - \frac {x(x + 1) - (x^2 + 1) + 3x} {x + 2} = \frac {- \, x(x + 1) + x^2 + 1 - 3x} {x + 2}\)
Příklad 4.12
| a) \(\displaystyle \frac {16} {2p^2 - 8p} - \frac {2} {p - 4}\) | b) \(\displaystyle p - \frac {p^2 - q} {p}\) |
Řešení
a) \(\displaystyle \frac {16} {2p^2 - 8p} - \frac {2} {p - 4} =
\frac {16} {2p(p - 4)} - \frac {2} {p - 4} = \frac {16 \cdot 1 - 2 \cdot 2p} {2p(p - 4)} =
\frac {16 - 4p} {2p(p - 4)} = \frac {4(4 - p)} {2p(p - 4)} = \)
\(\displaystyle = \frac {(-1) \cdot 4 \cdot (-1) \cdot (4 - p)} {2p(p - 4)} =
\frac {- \, 4(p - 4)} {2p(p - 4)} = \frac {- \, 4} {2p}\)
Výpočet má smysl za podmínky, že \(p \in \mathbb R - \{0; 4\}\).
b) \(\displaystyle p - \frac {p^2 - q} {p} = \; \frac {p} {1} - \frac {p^2 - q} {p} = \;
\frac {p \cdot p - (p^2 - q) \cdot 1} {p} = \; \frac {p^2 - (p^2 - q)} {p} = \frac {p^2 - p^2 + q} {p} = \;
\frac {q} {p}\)
Výpočet má smysl za podmínky, že \(p \in \mathbb R - \{0\}\), \(q \in \mathbb R\).
Při řešení úloh, ve kterých se objevují lomené výrazy, obvykle využíváme sčítání, násobení, vytýkání apod. Jelikož jsou lomené výrazy speciálním typem výrazů, lze je opět využít při řešení slovních úloh.
Příklad 4.13
| a) \(\displaystyle \left(\frac {2} {a + 1} - \frac {4a} {a^2 - 1}\right) \cdot \left(\frac {1} {a} - 1\right)\) | b) \(\displaystyle \frac {18a} {6a^2 - 6b^2} + \LARGE \frac {\Large \frac {ab \, - \, b^2} {a^3 \, + \, a^2b \, + \, 5a \, + \, 5b}} {\Large \frac {a^2 \, - \, 2ab \, + \, b^2} {3a^2 \, + \, 15}}\) |
Řešení
a) \(\displaystyle \left(\frac {2} {a + 1} - \frac {4a} {a^2 - 1}\right) \cdot
\left(\frac {1} {a} - 1\right) =
\left(\frac {2} {a + 1} - \frac {4a} {(a - 1)(a + 1)}\right) \cdot \left(\frac {1 - 1 \cdot a} {a}\right) =
\frac {2 \cdot (a - 1) - 4a} {(a + 1)(a - 1)} \cdot \frac {1 - a} {a} = \)
\(\displaystyle = \frac {2a - 2 - 4a} {(a + 1)(a - 1)} \cdot \frac {1 - a} {a} =
\frac {-2a - 2} {(a + 1)(a - 1)} \cdot \frac {1 - a} {a} =
\frac {-2(a + 1)} {(a + 1)(a - 1)} \cdot \frac {(a - 1) \cdot (-1)} {a} =
\frac {-2} {1} \cdot \frac {-1} {a} = \frac {2} {a}\)
Výpočet platí za podmínky, že \(a \in \mathbb R - \{-\, 1; 0; 1 \}\).
b) \(\displaystyle \frac {18a} {6a^2 - 6b^2} +
\LARGE \frac {\Large \frac {ab \, - \, b^2} {a^3 \, + \, a^2b \, + \, 5a \, + \, 5b}}
{\Large \frac {a^2 \, - \, 2ab \, + \, b^2} {3a^2 \, + \, 15}} \normalsize =
\frac {18a} {6a^2 - 6b^2} + \frac {ab - b^2} {a^3 + a^2b + 5a + 5b} \div
\frac {a^2 - 2ab + b^2} {3a^2 + 15} =\)
\(\displaystyle = \frac {18a} {6(a^2 - b^2)} + \frac {b(a - b)} {a^2(a + b) + 5(a + b)} \cdot
\frac {3a^2 + 15} {a^2 - 2ab + b^2} =
\frac {3a} {a^2 - b^2} + \frac {b(a - b)} {(a + b)(a^2 + 5)} \cdot
\frac {3(a^2 + 5)} {(a - b)^2} = \)
\(\displaystyle = \frac {3a} {(a - b)(a + b)} + \frac {b \cdot 3} {(a + b) \cdot (a - b)} =
\frac {3a + 3b} {(a - b)(a + b)} = \frac {3(a + b)} {(a - b)(a + b)} = \frac {3} {a -b}\)
Výpočet platí za podmínky, že \(a \in \mathbb R\), \(b \in \mathbb R\)
a zároveň \(a \neq \pm b\).
Příklad 4.14
Předpokládejme, že se tuňákové konzervy běžně prodávají v balení po \(x\) kusech, přičemž cena za balení činí
\(k\) Kč. V rámci mimořádné nabídky lze koupit za stejnou cenu větší balení, ve kterém je o \(y\) konzerv více než obvykle. Jakou částku lze využitím této akce ušetřit za každou tuňákovou konzervu?
Řešení
Ušetřenou částku (označíme ji \(u\)) vypočítáme jako rozdíl ceny za jednu konzervu bez slevy a ve slevě:
\(\displaystyle u = \frac {k} {x} - \frac {k} {x + y} = \frac {k \cdot (x + y) - k \cdot x} {x \cdot (x + y)} = \frac {kx + ky - kx} {x(x + y)} = \frac {ky} {x(x + y)}\)
Využitím mimořádné nabídky lze ušetřit \(\displaystyle \frac {ky} {x(x + y)}\) Kč za jednu konzervu.
Cvičení k této části.
