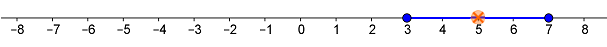\begin{align} \end{align}


1.3 Absolutní hodnota reálného čísla

Definice

Symbolem \(|a|\) označujeme absolutní hodnotu reálného čísla \(a\), přičemž platí:
1. pro \(a \geq 0\) je \(|a| = a\)
2. pro \(a < 0\) je \(|a| = - \, a\)

Absolutní hodnotu reálného čísla \(a\) lze interpretovat také geometricky. Představuje totiž vzdálenost obrazu čísla \(a\) od obrazu nuly na číselné ose.
absolutní hodnota

Mezi důležité vlastnosti absolutní hodnoty reálného čísla patří následující vlastnosti.

Pro všechna reálná čísla \(a\), \(b\) platí:
1. \(|a| \geq 0\) 2. \(|a| = |- \, a|\) 3. \(\sqrt{a \cdot a \;} = |a|\) 4. \(|a - b| = |b - a|\)
Zobrazit

Příklad 1.6

Vypočítej:
a) \(\displaystyle \left|- \, \frac {1} {8}\right|\) b) \(|8 - 7 \cdot 6|\) c) \(|9 \cdot 2 - 5|\) d) \(|-5 + (-11) - 7|\)

Řešení

a) \(\displaystyle \left|- \, \frac {1} {8}\right| = \frac {1} {8}\)

b) \(|8 - 7 \cdot 6| = |8 - 42| = |-34| = 34\)

c) \(|9 \cdot 2 - 5| = |18 - 5| = |13| = 13\)

d) \(|-5 + (-11) - 7| = |-5 - 11 - 7| = |-23| = 23\)


Příklad 1.7

Znázorni na číselné ose všechna reálná čísla, pro něž platí:

a) \(|a| \geq 3\) b) \(|a| < 1\) c) \(|a| < - \, 2,5\) d) \(|a - 1| > 4\) e) \(|5 - a| \leq 2\)

Řešení

a) Vzdálenost obrazu čísla \(a\) od obrazu nuly na číselné ose je větší nebo rovna \(3\).
absolutní hodnota

b) Vzdálenost obrazu čísla \(a\) od obrazu nuly na číselné ose je menší než \(1\).
absolutní hodnota

c) Vzdálenost obrazu čísla \(a\) od obrazu nuly na číselné ose je menší než \(- \, 2,5\). Nelze, vzdálenost nemůže být záporná.

d) Vzdálenost obrazu čísla \(a\) od obrazu \(1\) je větší než \(4\).
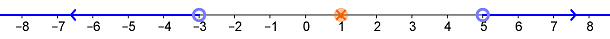
absolutní hodnota

e) Lze přepsat jako \(|a - 5| \leq 2\).
Vzdálenost obrazu čísla \(a\) od obrazu \(5\) je menší nebo rovna \(2\).
absolutní hodnota