Středová souměrnost
Definice
Středová souměrnost \(S(S)\) se středem v bodě S je zobrazení v rovině, ve kterém se zobrazí bod S na bod S'=S a každý bod X \neq S na bod X' tak, že bod S je středem úsečky XX'. Tedy platí, že |XS|=|SX'|.
Bod S se nazývá střed souměrnosti.
Zápisem \(S(S): X \rightarrow X'\) budeme rozumět, že bod X' je obrazem bodu X ve středové souměrnosti se středem v bodě S.
Následující applet znázorňuje, jak se zobrazují body ve středové souměrnosti. Zkusme si přemístit bod X a sledujme, jak se bude měnit poloha jeho obrazu.
Applet 3.1.1 - Středová souměrnost
Středová souměrnost je přímá shodnost.
Středová souměrnost je jednoznačně určena svým středem nebo dvojicí nesplývajících bodů X, X', kde bod X je vzor a bod X' je obraz bodu X. Středem souměrnosti je střed úsečky XX'.
Samodružné body
Při přemísťování bodu X v appletu 3.1.1 jsme mohli narazit na situaci, kdy nám „zmizela“ přímka XX'. Stalo se to ve chvíli, kdy bod X splynul s bodem S. Již z definice středové souměrnosti hned plyne, že jediným samodružným bodem středové souměrnosti je její střed.
Množinu všech samodružných bodů středové souměrnosti tvoří střed souměrnosti.
Samodružné přímky
Nyní budeme zkoumat, jak zobrazuje středová souměrnost přímku. Měňme polohu přímky p v následujícím appletu a sledujme, jak se změní její obraz. (Polohu přímky p změníme přemístěním bodů A a B.)
Applet 3.1.2 - Samodružné přímky
Pokud umístíme přímku p tak, že bod S leží na přímce p, tak se přímka p zobrazí sama na sebe. Samodružné přímky středové souměrnosti jsou všechny přímky, které procházejí středem souměrnosti.
Množinu všech samodružných přímek středové souměrnosti tvoří všechny přímky, které procházejí středem souměrnosti.
Středově souměrné útvary
Při řešení konstrukčních úloh za pomoci středové souměrnosti budeme často využívat vlastností konkrétních geometrických útvarů. Proto je dobré si připomenout některé útvary, které se při vhodné volbě středu souměrnosti zobrazí samy na sebe. Takovýmto útvarům se říká středově souměrné útvary .
Mezi středově souměrné útvary patří například čtverec, kosočtverec, kružnice, obdélník nebo kosodélník. Středem souměrnosti kružnice je její střed, středem souměrnosti ostatních vyjmenovaných útvarů je průsečík jejich úhlopříček.
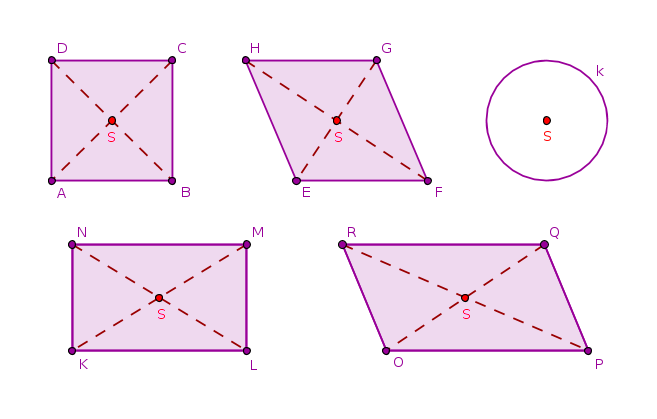
Obr. 3.1.1 - Středově souměrné útvary
Příklady
