\begin{align}
\end{align}
Úloha 4
Sestrojte všechny rovnoramenné trojúhelníky \(ABC\) se základnou \(AB\) a výškou na základnu délky \(v_c\) cm, \(v_c > 0\), aby \(|AB|:|BC|=2:3\).
Nápověda: 
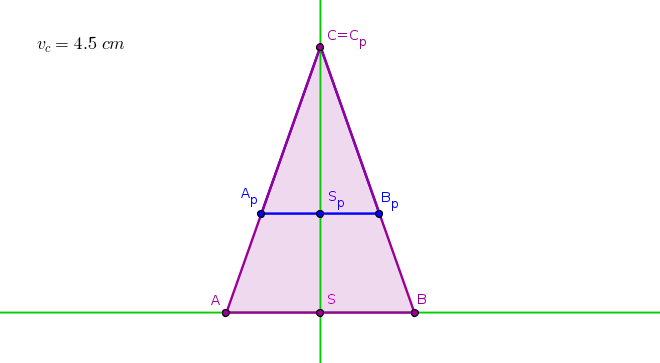
Obr. 5.3.1 - Náčrtek úlohy 4
Trojúhelník \(ABC\) nemůžeme sestrojit přímo, neznáme délky stran. Sestrojíme proto pomocný trojúhelník \(A_pB_pC_p\), pro který bude platit \(|A_pB_p|:|B_pC_p|=2:3\) (zvolíme například délku stran \(2\) cm a \(3\) cm), který ve vhodné stejnolehlosti zobrazíme na trojúhelník požadovaných vlastností.
Pro výšku \(C_pS_p\) na základnu pomocného trojúhelníka a výšku \(CS\) na základnu trojúhelníka \(ABC\) musí platit \(|CS|=\kappa\cdot|C_pS_p|\), zvolme například bod \(C_p=C\) jako střed stejnolehlosti, a protože známe délku výšky \(CS\), můžeme zkonstruovat trojúhelník \(ABC\).

Konstrukce a zápis konstrukce
Applet 5.3.1 - Úloha 4
Diskuse
Úloha má dvě řešení.
Další úlohy



