Podobná zobrazení
Definice
Zobrazení \(f\) v rovině je podobné zobrazení, jestliže existuje číslo \(k > 0\), že pro každé dva body \(X\), \(Y\) roviny a jejich obrazy \(X'\), \(Y'\) platí \(|X'Y'|=k\cdot |XY|\).
Podobné zobrazení se také nazývá podobnost.
Číslo \(k\) se nazývá koeficient podobnosti.
Všimněme si, že pro \(k=1\) je definice podobného zobrazení stejná jako definice shodného zobrazení. Shodné zobrazení je jen speciálním případem podobného zobrazení.
Podobné zobrazení s koeficientem podobnosti \(k=1\) je shodné zobrazení.
Každé podobné zobrazení je prosté.
Obdobně jako u shodného zobrazení v každém podobném zobrazení s koeficientem podobnosti \(k\) platí:
- Obrazem každé úsečky \(AB\) je úsečka \(A'B'\), pro kterou platí \(|A'B'|=k\cdot |AB|\).
- Obrazem každé přímky \(AB\) je přímka \(A'B'\), obrazy rovnoběžných přímek jsou rovnoběžné přímky.
- Obrazem každého úhlu \(AVB\) je úhel \(A'V'B'\) s ním shodný.
Podobné útvary
Definice
Podobné útvary jsou takové útvary, pro které existuje číslo \(k>0\) takové, že pro dvojici libovolných bodů \(A\), \(B\) jednoho útvaru a odpovídající dvojici bodů \(A'\), \(B'\) druhého útvaru platí \(|A'B'|=k\cdot|AB|\).
Číslo \(k\) v definici podobného útvaru je koeficientem podobnosti útvarů.
Například na následujícím obrázku jsou trojúhelníky \(ABC\) a \(A'B'C'\) podobné. Z obrázku je vidět, že odpovídající si úhly podobných trojúhelníků jsou shodné.
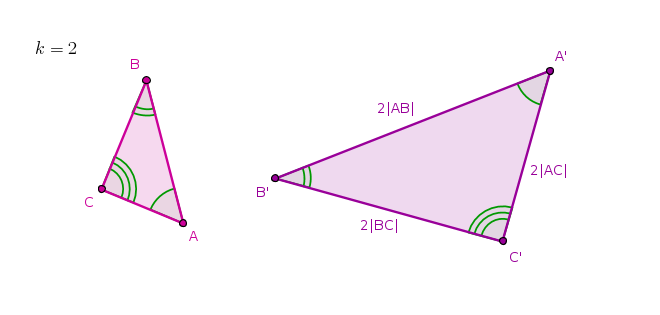
Obr. 4.0.1 - Podobné útvary
Pokud je zobrazení \(f\) podobné, pak je obrazem každého útvaru útvar s ním podobný.
Přímá a nepřímá podobnost
Přímou a nepřímou podobnost definujeme analogicky jako přímou a nepřímou shodnost.
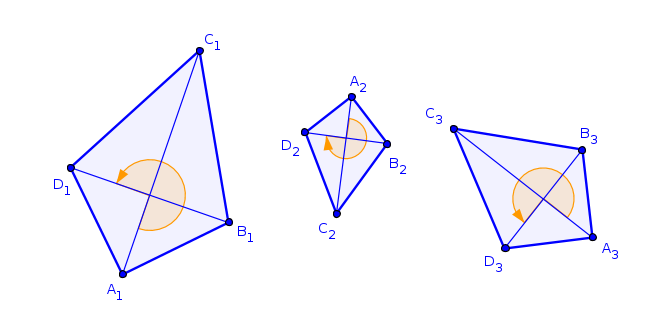
Obr. 4.0.2 - Podobnosti
Dva útvary nazveme přímo podobné, jsou-li podobné, kde jejich vrcholy jsou značeny v abecedním pořadí proti směru hodinových ručiček (obr 4.0.2 - deltoidy \(A_1B_1C_1D_1\) a \(A_3B_3C_3D_3\)). V opačném případě nazveme útvary nepřímo podobné (obr 4.0.2 - deltoidy \(A_1B_1C_1D_1\) a \(A_2B_2C_2D_2\)).
Definice
Přímá podobnost je každá podobnost, ve které jsou libovolný trojúhelník a jeho obraz přímo podobné.
Nepřímá podobnost je každá podobnost, ve které jsou libovolný trojúhelník a jeho obraz nepřímo podobné.
Podobnostmi, které jsou shodnostmi, jsme se již zabývali v předchozí kapitole. V této kapitole se dále budeme zabývat stejnolehlostmi.
