Stejnolehlost
Definice
Stejnolehlost \(H(S, \kappa)\) (neboli homotetie) určená bodem \(S\) a nenulovým reálným číslem \(\kappa\) je zobrazení v rovině, ve kterém se zobrazí bod \(S\) na bod \(S'=S\) a každý bod \(X \neq S\) na bod \(X'\) tak, že \(|X'S|=|\kappa| \cdot |XS|\).
Pro \(\kappa >0\) leží bod \(X'\) na polopřímce \(SX\).
Pro \(\kappa <0\) leží bod \(X'\) na polopřímce opačné k polopřímce \(SX\).
Bod \(S\) se nazývá střed stejnolehlosti, číslo \(\kappa\) se nazývá koeficient stejnolehlosti.
Zápisem \(H(S, \kappa): X \rightarrow X'\) budeme rozumět, že bod X' je obrazem bodu X ve stejnolehlosti se středem \(S\) a koeficientem \(\kappa\).
Applet 4.1.1 - Stejnolehlost
Stejnolehlost je přímá podobnost s koeficientem \(k=|\kappa|\).
Stejnolehlost je jednoznačně určena středem \(S\) a koeficientem \(\kappa\) nebo středem \(S\) a dvojicí bodů \(X\), \(X'\), kde \(X\) je vzor a \(X'\) obraz bodu \(X\), přitom \(X\), \(X' \neq S\).
Poznámka
Středová souměrnost se středem \(S\) je speciálním případem stejnolehlosti se středem \(S\) a koeficientem \(\kappa =-1\).
Samodružné body
Z definice přímo plyne, že samodružným bodem stejnolehlosti je střed stejnolehlosti \(S\).
Neexistuje koeficient \(\kappa\), pro který by stejnolehlost měla nějaké další samodružné body? 
Množinu všech samodružných bodů stejnolehlosti tvoří její střed \(S\) pro koeficient \(\kappa \neq 1\), nebo je to celá rovina pro koeficient \(\kappa = 1\).
Samodružné přímky
Zkusme v následujícím appletu získat nějaké samodružné přímky. Můžeme měnit koeficient \(\kappa\) i polohu přímky \(p\) a středu stejnolehlosti \(S\).
Applet 4.1.2 - Samodružné přímky
Samodružné přímky jsme mohli získat pouze ve dvou speciálních případech:
- koeficient \(\kappa = 1\),
- nebo přímka \(p\) prochází středem \(S\) stejnolehlosti.
Množina všech samodružných přímek stejnolehlosti je tvořena všemi přímkami, které prochází středem \(S\) stejnolehlosti, nebo je to celá rovina pro koeficient \(\kappa = 1\).
Příklady
Stejnolehlost kružnic
Zamysleme se, co je obrazem kružnice \(k\) ve stejnolehlosti \(H(S, \kappa)\). Pomůže nám k tomu následující applet. Pohybujme bodem \(X\) na kružnici \(k\) a pozorujme, co vytvoří obrazy bodů.
Applet 4.1.8 - Stejnolehlost kružnic
Obrazem kružnice \(k\) se středem \(O\) a poloměrem \(r\) ve stejnolehlosti určené středem \(S\) a koeficientem \(\kappa\) je kružnice \(k'\) se středem \(O'\) a poloměrem \(|\kappa|\cdot r\), přitom bod \(O'\) je obrazem bodu \(O\).
Každé dvě kružnice jsou stejnolehlé. Střed \(O\) kružnice \(k\) se zobrazí na střed \(O'\) kružnice \(k'\) tak, že \(|O'S|=|\kappa|\cdot|OS|\). Libovolný bod \(X\) na kružnici \(k\) se v dané stejnolehlosti zobrazí na bod \(X'\) takový, že \(|X'S|=|\kappa|\cdot|XS|\). Z podobnosti trojúhelníků \(SOX\) a \(SO'X'\) plyne \(|O'X'|=|\kappa|\cdot|OX|\).
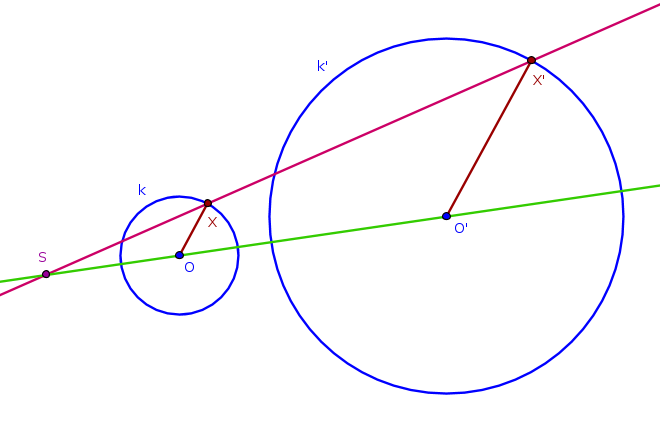
Obr. 4.1.5 - Stejnolehlost kružnic
U stejnolehlosti kružnic nás bude zajímat střed stejnolehlosti, který zobrazí jednu kružnici na druhou, a společné tečny dvou kružnic. Tyto problémy jsou detailněji rozebrány v příkladech.
Příklady na stejnolehlost kružnic
