Příklad 2
Jsou dány kružnice \(k_1\) se středem \(O_1\), \(k_2\) se středem \(O_2\). Sestrojte přímku \(t\) takovou, aby byla přímka \(t\) tečnou kružnice \(k_1\) a zároveň tečnou kružnice \(k_2\).
Rozbor
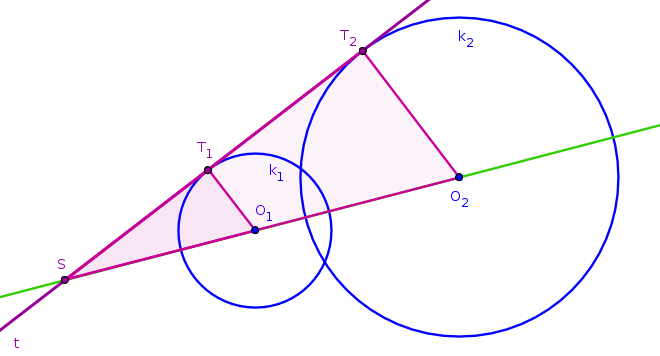
Obr. 4.1.7 - Náčrtek příkladu 2
Než začnete řešit tento příklad, pokuste se vyřešit předchozí příklad.
- Předpokládejme, že taková tečna existuje (obr. 4.1.7). Pak bude existovat bod \(T_1\) na kružnici \(k_1\) takový, že tečna \(t\) bude kolmá na \(T_1O_1\) (jinak by existovalo více průsečíků přímky \(t\) a kružnice \(k_1\) a přímka \(t\) by byla sečnou kružnice \(k_1\)). Analogicky bude existovat bod \(T_2\) na kružnici \(k_2\) (obr. 4.1.7).
- Průsečík přímky \(O_1O_2\) a tečny \(t\) označme \(S\). Pak platí, že trojúhelník \(ST_1O_1\) je podobný trojúhelníku \(ST_2O_2\). Trojúhelník \(ST_2O_2\) získáme jako obraz trojúhelníka \(ST_1O_1\) ve stejnolehlosti se středem \(S\) a koeficientem \(k=\frac{|O_2T_2|}{|O_1T_1|}\). V této stejnolehlosti je kružnice \(k_2\) obrazem kružnice \(k_1\).
- Abychom mohli sestrojit tečnu \(t\), potřebujeme sestrojit dva její body. Bod \(S\), střed dané stejnolehlosti, umíme získat - postupujeme stejně jako v předchozím příkladě.
- Dále nám stačí určit jeden z bodů \(T_1\), \(T_2\). Takový bod nalezneme snadno, víme, že úhel \(ST_1O_1\) (resp. \(ST_2O_2\)) je pravý, takže využijeme Thaletovu kružnici.
Konstrukce a zápis konstrukce
Applet 4.1.10 - Příklad 2
Poznámka
Pokud mají kružnice \(k_1\), \(k_2\) stejný poloměr, pak existují dvě tečny kružnic rovnoběžné s přímkou \(O_1O_2\), které nezískáme pomocí stejnolehlosti (neexistuje průsečík tečny a přímky \(O_1O_2\)). Tyto tečny získáme tak, že vedeme kolmici k přímce \(O_1O_2\) bodem \(O_1\) (resp. \(O_2\)). Tečna je rovnoběžka s přímkou \(O_1O_2\) vedená průsečíkem kolmice a kružnice \(k_1\) (resp. \(k_2\)).
Diskuse
- Úloha má 4 řešení, pokud kružnice \(k_1\), \(k_2\) nejsou soustředné a nemají žádný společný bod.
- Úloha má 3 řešení, pokud kružnice \(k_1\), \(k_2\) nejsou soustředné, dotýkají se v jednom společném bodě a střed kružnice \(k_1\) (resp. \(k_2\)) neleží ve vnitřní oblasti kružnice \(k_2\) (resp. \(k_1\)).
- Úloha má 2 řešení, pokud kružnice \(k_1\), \(k_2\) nejsou soustředné a existují dva průsečíky kružnic \(k_1\), \(k_2\).
- Úloha má 1 řešení, pokud kružnice \(k_1\), \(k_2\) nejsou soustředné, dotýkají se v jednom společném bodě a střed kružnice \(k_1\) (resp. \(k_2\)) leží ve vnitřní oblasti kružnice \(k_2\) (resp. \(k_1\)).
- Úloha má nekonečně mnoho řešení, pokud jsou kružnice \(k_1\), \(k_2\) totožné.
- Úloha jinak nemá řešení.
Další příklady
| Příklad 1 | Příklad 2 |
