Orientovaný úhel
S pojmem úhel jsme se zajisté již v geometrii setkali. Úhel \(AVB\) chápeme jako část roviny, která je ohraničená dvěma polopřímkami \(VA\), \(VB\). Polopřímky \(VA\), \(VB\) se nazývají ramena úhlu. Zavedeme si teď nový pojem, který budeme později používat.
Definice
Orientovaný úhel je úhel, u kterého je určeno, které jeho rameno je počáteční a které je koncové.
Orientace úhlu \(AVB\) je dána pořadím písmen v jeho zápisu, počáteční rameno je rameno \(VA\) a koncové rameno je rameno \(VB\).
Orientace úhlu se někdy vyznačuje obloučkem se šipkou vedoucí od počátečního ramene ke koncovému (obr. 2.3.1).
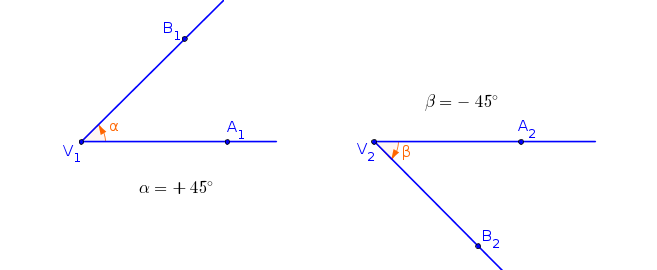
Obr. 2.3.1
Počáteční a koncové rameno orientovaného úhlu si můžeme představit jako hodinové ručičky. Koncové rameno se může otáčet kolem vrcholu úhlu buď po směru pohybu hodinových ručiček nebo proti směru. Podle směru pohybu hovoříme o kladném, resp. záporném smyslu otáčení. Pokud se koncové rameno otáčí proti směru pohybu ručiček, hovoříme o kladném smyslu otáčení (obr. 2.3.1 vlevo), pokud se otáčí ve směru pohybu hodinových ručiček, hovoříme o záporném smyslu otáčení (obr. 2.3.1 vpravo). Smysl otáčení dáváme najevo znaménkem uvedeným u velikosti úhlu. Je-li znaménko kladné, jde o kladný smysl otáčení, je-li znaménko záporné, jde o záporný smysl otáčení (obr. 2.3.1). Tuto myšlenku potřebujeme k zavedení pojmu základní velikost orientovaného úhlu.
Definice
Základní velikost orientovaného úhlu \(AVB\) je velikost úhlu \(AVB\), který vytvoří polopřímka \(VA\) otočením v kladném smyslu do polopřímky \(VB\).
Základní velikost orientovaného úhlu je tedy číslo z intervalu \(\left \langle 0; 360°\right)\), tedy \(\left \langle 0; 2\pi \right)\) v radiánech. Jestliže počáteční rameno orientovaného úhlu splývá s koncovým, nazýváme tento úhel nulový orientovaný úhel.
Pojem základní velikost zavádíme proto, že velikost orientovaného úhlu \(AVB\) je každá hodnota \(\alpha + k\cdot 360°\), příp. \(\alpha + k\cdot 2\pi\), kde \(\alpha\) je základní velikost úhlu \(AVB\) a \(k\) je libovolné celé číslo.
Orientované úhly \(\alpha\), \(\beta\) jsou shodně orientované, pokud mají stejný smysl otáčení, tj. oba úhly mají kladný smysl otáčení, nebo mají oba záporný smysl otáčení.
V následujícím obrázku jsou orientované úhly \(\alpha = B_1V_1A_1\), \(\beta = A_2V_2B_2\) shodně orientované, úhly \(\alpha = B_1V_1A_1\), \(\gamma = A_3V_3B_3\) nejsou shodně orientované.
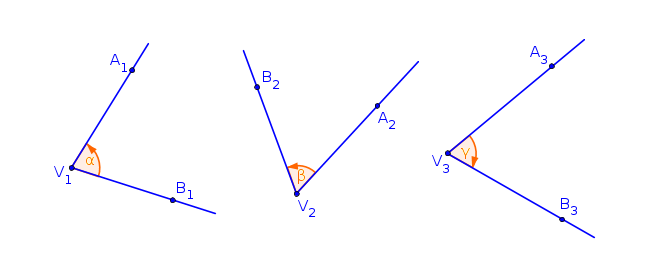
Obr. 2.3.2
