Samodružné prvky
Pod pojmem samodružné prvky zobrazení \(f\) budeme rozumět samodružné body a samodružné přímky daného zobrazení.
Definice
Je dáno zobrazení \(f\) v rovině.
Samodružný bod zobrazení \(f\) je takový bod \(X\), který se zobrazí sám na sebe, tj. \(f(X)=X\).
Samodružná přímka zobrazení \(f\) je taková přímka \(p\), která se zobrazí sama na sebe, tj. \(f(p)=p\).
Příklady
Příklad 1
Podívejme se na následující obrázek, kde se čtverec \(ABCD\) v zobrazení \(f\) zobrazil na kosodélník \(A'B'C'D'\).
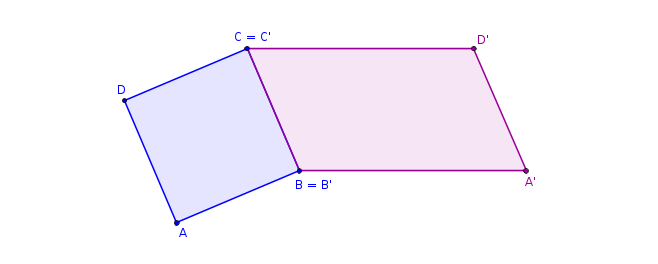
Obr. 2.1.1
Určete samodružné prvky daného zobrazení. 
Příklad 2
Čtverec \(ABCD\) se v zobrazení \(f\) zobrazil na čtverec \(A'B'C'D'\).
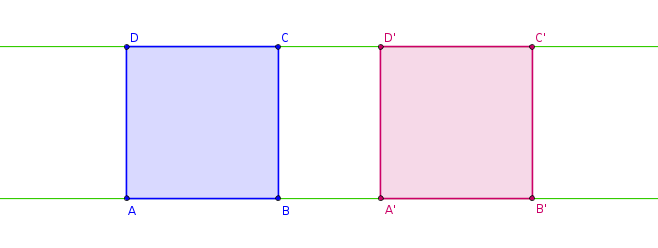
Obr. 2.1.2
Určete samodružné prvky daného zobrazení. 
