Shodná zobrazení
Definice
Zobrazení \(f\) v rovině je shodné zobrazení, jestliže pro každé dva body \(X\), \(Y\) roviny a jejich obrazy \(X'\), \(Y'\) platí \(|XY|=|X'Y'|\).
Shodné zobrazení v rovině se rovněž nazývá shodnost.
Z definice shodného zobrazení plyne, že každé shodné zobrazení je prosté.
Speciálním případem shodného zobrazení je identické zobrazení, které každému bodu \(X\) roviny přiřazuje ten samý bod \(f(X) = X\).
Identické zobrazení se rovněž nazývá identitou.
Protože je každý bod v identitě samodružný, je i každá přímka samodružná.
V každém shodném zobrazení platí:
- Obrazem každé úsečky \(AB\) je úsečka \(A'B'\) s ní shodná, tj. má stejnou délku.
- Obrazem každé přímky \(AB\) je přímka \(A'B'\), obrazy rovnoběžných přímek jsou rovnoběžné přímky.
Shodné útvary
Definice
Shodné útvary jsou takové útvary, které je možno přemístit tak, že se kryjí.
Například trojúhelník \(ABC\) se přemístí na trojúhelník \(A'B'C'\) na obr. 3.0.1. (Tj. bod \(A\) se přemístí do bodu \(A'\), bod \(B\) do bodu \(B'\) a bod \(C\) do bodu \(C'\).) Z obrázku je vidět, že odpovídající si strany shodných trojúhelníků jsou shodné a že odpovídající si úhly shodných trojúhelníků jsou shodné, což plyne přímo z definice shodných útvarů.
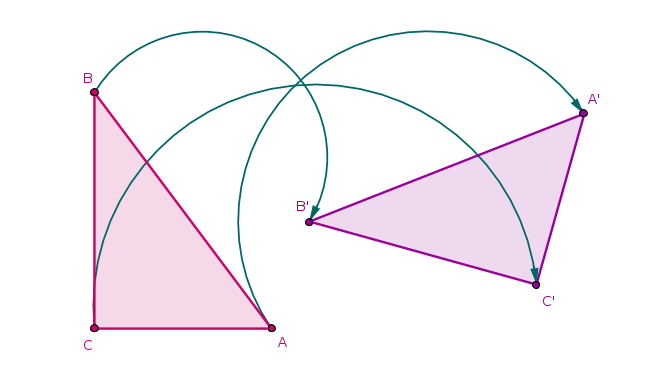
Obr. 3.0.1 - Shodné útvary
Pokud je zobrazení \(f\) shodné, pak je obrazem každého útvaru útvar s ním shodný.
Přímá a nepřímá shodnost
Prohlédněme si teď čtyřúhelníky v následujícím obrázku, všechny čtyřúhelníky jsou shodné.

Obr. 3.0.2 - Shodnosti
Všimněme si rozdílu mezi jednotlivými čtyřúhelníky. Čtyřúhelníky \(A_1B_1C_1D_1\) a \(A_2B_2C_2D_2\) jsou shodné, přičemž jejich vrcholy jsou značeny v abecedním pořadí proti směru hodinových ručiček. V takovém případě říkáme, že jsou čtyřúhelníky přímo shodné. Čtyřúhelníky \(A_1B_1C_1D_1\) a \(A_3B_3C_3D_3\) nejsou přímo shodné, neboť vrcholy čtyřúhelníka \(A_3B_3C_3D_3\) bychom museli číst po směru pohybu hodinových ručiček, abychom je přečetli v abecedním pořadí. Čtyřúhelníky \(A_1B_1C_1D_1\) a \(A_3B_3C_3D_3\) jsou nepřímo shodné.
Definice
Přímá shodnost je každá shodnost, ve které jsou libovolný trojúhelník a jeho obraz přímo shodné.
Nepřímá shodnost je každá shodnost, ve které jsou libovolný trojúhelník a jeho obraz nepřímo shodné.
My se budeme dále podrobněji zabývat těmito shodnostmi:
- středová souměrnost,
- osová souměrnost,
- posunutí,
- otočení.
