Příklad 7
Sestrojte všechny trojúhelníky ABC, je-li dána strana a, těžnice na stranu b a velikost úhlu \(\alpha = 45°\).
Rozbor
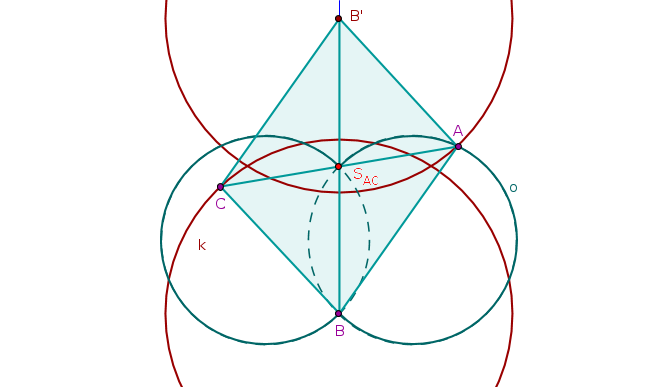
Obr. 3.1.8 - Náčrtek příkladu 7
Tento příklad budeme řešit podobně jako příklad předchozí.
- Uvědomíme si, že trojúhelník ABC je část kosodélníka ABCB'.
- Trochu obtížnější bude zjistit polohu bodu A. K tomu budeme muset najít množinu bodů, odkud je úsečka BS_{AC} vidět pod úhlem 45°. K sestrojení této množiny využijeme obvodového úhlu.

Applet 3.1.9 - Obvodový úhel
- My potřebujeme, aby u vrcholu A byl úhel velikosti 45°. Sestrojíme proto množinu bodů, odkud je úsečka BS_{AC} vidět pod tímto úhlem.
- Protože je ale tento úhel obvodový, příslušný středový úhel oblouku kružnice, na kterém bude ležet bod A trojúhelníka ABS_{AC}, musí mít velikost 90°. Střed takovéto kružnice nalezneme pomocí Thaletovy kružnice nad průměrem BS_{AC}.
- Bod A bude průsečíkem obrazu kružnice k ve středové souměrnosti se středem v bodě S_{AC} a množiny bodů v rovině, odkud je vidět úsečka BS_{AC} pod úhlem o velikosti 45°.
Konstrukce a zápis konstrukce
Applet 3.1.10 - Příklad 7
Diskuse
- Úloha má 4 řešení, pokud existují čtyři různé průsečíky kružnice k' a oblouku o.
- Úloha má 2 řešení, pokud existují pouze dva průsečíky kružnice k' a oblouku o, případně pokud existují průsečíky tři.
- Úloha nemá řešení, pokud neexistuje průsečík kružnice k' a oblouku o.
Příklady
| Příklad 1 | Příklad 2 | Příklad 3 | Příklad 4 | Příklad 5 | Příklad 6 | Příklad 7 |
