Příklad 5
Jsou dány rovnoběžné přímky \(a\), \(c\) a bod \(D\). Sestrojte deltoid \(ABCD\) s pravým úhlem u vrcholu \(D\) tak, aby body \(A\), \(B\) ležely na přímce \(a\) a bod \(C\) ležel na přímce \(c\). Hlavní úhlopříčka deltoidu je úhlopříčka \(BD\).
Rozbor
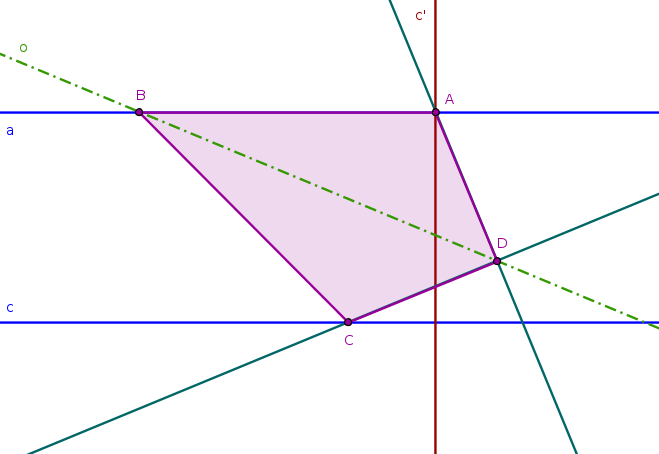
Obr. 3.4.4 - Náčrtek příkladu 5
- Bod \(C\) deltoidu \(ABCD\) leží na přímce \(c\). Obrazem bodu \(C\) v otočení určeném středem otočení \(D\) a úhlem velikosti \(90°\), neboť úhel u vrcholu \(D\) deltoidu má být pravý, je bod \(A\). Proto bude bod \(A\) ležet na obrazu \(c'\) přímky \(c\) v otočení popsaném výše.
- Bod \(A\) je průsečík přímky \(c'\) a přímky \(a\).
- Protože má být u vrcholu \(D\) pravý úhel, bude bod \(C\) ležet na kolmici k přímce \(AD\) procházející bodem \(D\).
- Bod \(C\) je průsečík této kolmice a přímky \(c\).
- Deltoid je osově souměrný podle hlavní úhlopříčky. Hlavní úhlopříčka deltoidu bude ležet na ose úhlu \(CDA\).
- Bod \(B\) je průsečík osy úhlu \(CDA\) a přímky \(a\).
Konstrukce a zápis konstrukce
Applet 3.4.7 - Příklad 5
Diskuse
Počet řešení závisí na umístění bodu \(D\) vzhledem k přímkám \(a\), \(c\). Označme si \(x\) osu pásu určeném přímkami \(a\), \(c\).
- Úloha má dvě řešení, pokud bod \(D\) leží ve stejné polorovině určené hraniční přímkou \(x\) jako přímka \(c\).
- Úloha nemá řešení, pokud bod \(D\) leží na přímce \(x\), nebo na přímce \(c\).
Pokud bod \(D\) leží v opačné polorovině, výsledné obrazce budou tvořit nekonvexní osově souměrný čtyřúhelník, nebude to ale deltoid. Pokud bude bod \(D\) ležet na přímce \(c\), výsledný obrazec opět nebude deltoid, bude to čtverec.
Další příklady
| Příklad 1 | Příklad 2 | Příklad 3 | Příklad 4 | Příklad 5 | Příklad 6 |
