Příklad 3
Je dána přímka \(p\), kružnice \(k\) a bod \(S_{BD}\). Sestrojte všechny čtverce \(ABCD\) tak, aby bod \(A\) ležel na přímce \(p\), bod \(B\) ležel na kružnici \(k\) a bod \(S_{BD}\) byl střed úhlopříčky \(BD\).
Rozbor
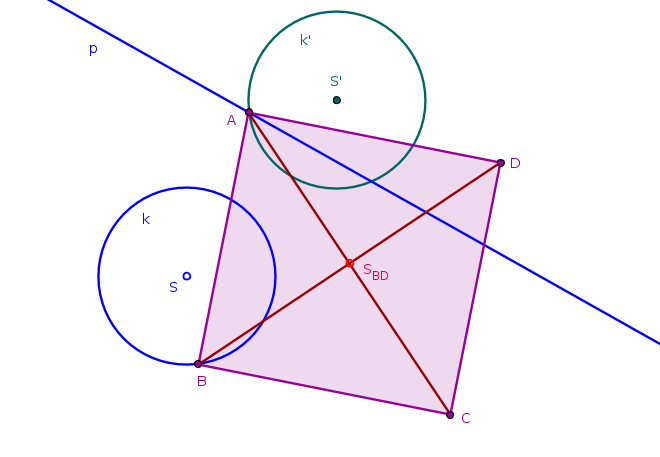
Obr. 3.4.2 - Náčrtek příkladu 3
Střed \(S_{BD}\) úhlopříčky \(BD\) je střed čtverce. Víme, že všechny vrcholy čtverce jsou od středu stejně vzdálené a že úhlopříčky čtverce svírají pravý úhel.
- Bod \(B\) leží na kružnici \(k\), proto bude bod \(A\) ležet na obrazu \(k'\) kružnice \(k\) v otočení určeném středem otočení \(S_{BD}\) a pravým úhlem.
- Bod \(A\) je průsečík kružnice \(k'\) a přímky \(p\).
- Bod \(B\) leží na kružnici \(k\) a získáme ho otočením bodu \(A\) o úhel velikosti \(90°\) okolo středu čtverce.
- Body \(C\), \(D\) sestrojíme snadno, víme, že úhlopříčky čtverce se půlí.
Konstrukce a zápis konstrukce
Applet 3.4.5 - Příklad 3
Diskuse
- Úloha má 4 řešení, pokud existují čtyři průsečíky obrazu \(k'\) kružnice \(k\) v daném otočení (v kladném i záporném smyslu) s přímkou \(p\).
- Úloha má 3 řešení, pokud existují tři průsečíky kružnice \(k'\) s přímkou \(p\).
- Úloha má 2 řešení, pokud existují dva průsečíky kružnice \(k'\) s přímkou \(p\).
- Úloha má 1 řešení, pokud existuje jeden průsečík kružnice \(k'\) s přímkou \(p\).
- Úloha nemá jinak řešení.
Další příklady
| Příklad 1 | Příklad 2 | Příklad 3 | Příklad 4 | Příklad 5 | Příklad 6 |
