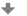Elipsa
Elipsa je geometrický útvar, o kterém jsme jistě už mnohokrát slyšeli. Připomeňme si například první Keplerův zákon, který říká, že planety obíhají okolo Slunce po elipsách málo odlišných od kružnic, v jejichž společném ohnisku je Slunce.
Obrázek 4.8: První Keplerův zákon
V obr. 4.8 je zobrazen pohyb planety okolo Slunce, které se nachází v ohnisku \(E\) elipsy \(e\). Vidíme, že vzdálenost planety od Slunce, tj. vzdálenost \(x_1\) se však při pohybu po elipse mění. Současně se však mění i vzdálenost \(x_2\). Připomeňme definici elipsy, kterou známe z [12] analytické geometrie, jako množinu bodů definovanou pomocí pojmu vzdálenost.
Definice
Mějme dány dva různé body \(E\) a \(F\) takové, že platí \(2a>|EF|\). Množina všech bodů, které mají od bodů \(E\) a \(F\) součet vzdáleností roven \(2a\), se nazývá elipsa; značíme ji e.
Symbolicky výše uvedenou definici zapisujeme e=\{X\in E_2; |XE|+|XF|=2a\}. Konstanta \(a\) je délka hlavní poloosy.
Obrázek 4.9: Elipsa s vyznačenými délkami \(a\), \(b\) a \(e\)
Na obr. 4.9 jsou zobrazeny důležité charakteristiky elipsy:
- bod \(S\): střed elipsy,
- přímka \(EF\): hlavní osa elipsy,
- body \(A, B\) elipsy ležící na přímce \(EF\): hlavní vrcholy elipsy,
- přímka kolmá k hlavní ose procházející středem: vedlejší osa elipsy,
- body \(C, D\) elipsy ležící na vedlejší ose: vedlejší vrcholy elipsy,
- úsečka spojující hlavní vrchol elipsy a střed, tj. \(AS, BS\): hlavní poloosa,
- úsečka spojující vedlejší vrchol elipsy a střed, tj. \(CS, DS\): vedlejší poloosa,
- úsečka spojující ohnisko elipsy a střed, tj. \(ES, FS\): excentricita, výstřednost.
Délku hlavní poloosy značíme \(a\), vedlejší poloosy \(b\) a vzdálenost ohnisek od středu elipsy značíme \(e\), viz obr. 4.9. Pro uvedené délky úseček platí vztah
a^2=e^2+b^2.
Již v úvodu této kapitoly bylo zmíněno, že elipsa úzce souvisí s kružnicí. V appletu na obr. 4.9 pohybujte ohnisky tak, aby vznikl útvar co nejbližší kružnici. Může se z elipsy stát kružnice? 
Příklad 4.3.1
V appletu na obr. 4.11 je zobrazena hlavní poloosa elipsy, hlavní vrcholy \(A\) a \(B\) a ohniska \(E\) a \(F\). Bod \(X_1\), resp. \(X_2\), je průsečíkem kružnic \(k_1\) a \(k_2\) tak, aby \(k_1(E, |AR|)\) a \(k_2(F, |BR|)\). Bod \(R\) leží na úsečce \(EF\) a lze s ním pohybovat. Při pohybu bodem \(R\) se vykresluje stopa bodu \(X_1\), resp. \(X_2\). Na základě appletu ověřte, že vzniklá množina bodů je skutečně elipsa.
Obrázek 4.11: Applet - konstrukce elipsy
Vzniklá množina bodů je elipsa, jelikož bod \(X_1\), resp. \(X_2\), vznikl jako průsečík kružnic \(k_1\) a \(k_2\).
Bod \(X_1\) má od ohniska \(E\) vzdálenost rovnou poloměru kružnice \(k_1\) a od ohniska \(F\) vzdálenost rovnou poloměru kružnice \(k_2\), tj. \(|X_1E|=|AR|\) a \(|X_1F|=|BR|\). Bod \(R\) leží na úsečce \(AB\), jejíž délku označíme \(2a\), potom platí
|X_1E|+|X_1F|=|AR|+|RB|=|AB|=2a,
což splňují všechny body elipsy. Stejné vztahy platí pro bod \(X_2\). Z konstrukce je zřejmé, že žádný jiný bod kromě průsečíků kružnic \(k_1, k_2\) tuto vlastnost nesplňuje. Vzniklý útvar tedy opravdu je elipsa.
Elipsa jako množina středů kružnic
Následující text byl inspirován publikací [7].
V předchozí kapitole jsme hledali parabolu jako množinu středů kružnic, které se dotýkají řídicí přímky a prochází ohniskem. Nyní se budeme věnovat úkolu o něco náročnějšímu.
Příklad 4.3.2
Mějme zadané dva různé body - ohniska \(E\) a \(F\), a dvě kružnice \(k_1(E, r_1)\), \(k_2(F, r_2)\), tak aby vzdálenost ohnisek byla menší, než součet poloměrů kružnic, tj. \(|EF| < r_1+r_2\). Hledejme nyní množinu středů takových kružnic \(k\), které mají s jednou z kružnic \(k_1\), nebo \(k_2\) vnitřní dotyk a s druhou dotyk vnější.
Využijte applet na obr. 4.13, ve kterém lze pomocí bodu \(D\) měnit poloměr kružnice \(k_2\) a polohu ohniska \(F\). Pohybujte bodem \(A\) po kružnici \(k_2\) a pozorujte, jaký útvar vykreslí střed kružnice \(k\) a jak se situace změní při změně polohy bodů \(D\) a \(F\). Zaškrtávacím políčkem lze zobrazit, jakým způsobem byl bod \(X\) zkonstruován.
Obrázek 4.13: Applet - elipsa jako množina středů kružnic
V appletu na obr. 4.13 vidíme, že množina středů kružnic, které danou podmínku splňují je zřejmě elipsa. Při přibližování ohnisek se elipsa více podobá kružnici, což odpovídá poznatku rozebranému výše. Pokud se zvětší poloměr kružnice \(k_2\), zvětší se i velikost hlavní a vedlejší poloosy elipsy, a leží-li kružnice \(k_2\) uvnitř kružnice \(k_1\), leží i celá elipsa uvnitř kružnice \(k_1\).
Dále si můžeme všimnou, že nachází-li se bod \(A\) uvnitř kružnice \(k_1\), kružnice \(k\) má s kružnicí \(k_1\) vnitřní dotyk a s kružnicí \(k_2\) vnější dotyk, zatímco nachází-li se bod \(A\) vně kružnice \(k_1\), kružnice \(k\) má s kružnicí \(k_1\) vnější dotyk a s kružnicí \(k_2\) vnitřní dotyk.
Dokažme nyní, že útvar, který vznikl v appletu na obr. 4.13 je skutečně elipsa.
Obrázek 4.14: Elipsa jako množina středů kružnic
Pro elipsu musí z definice platit vztah e=\{X\in E_2; |XE|+|XF|=2a\}. V obr. 4.14 jsou vyznačeny poloměry hledaných kružnic. Zaměříme se nyní na bod \(X_1\), který je středem kružnice, která je uvnitř kružnice \(k_1\). Vzdálenost \(X_1, E\) lze vyjádřit pomocí poloměru zadané kružnice následujícím způsobem.
|X_1E|=|K_1E|-|K_1X_1|=r_1-d_1
Obdobným způsobem lze vyjádřit i vzdálenost \(X_1F\).|X_1F|=r_2+d_1
Jejich součet je tedy|X_1E|+|X_1F|=r_1-d_1 + r_2+d_1=r_1+r_2,
což je konstantní hodnota. Musí tedy platit rovnosti2a=r_1+r_2 \Rightarrow a=\frac{1}{2}(r_1+r_2) .
Obdobným způsobem lze postupovat pro bod \(X_2\), který je středem kružnice ležící uvnitř kružnice \(k_2\).
|X_2E|+|X_2F|=r_1+d_2 + r_2-d_2=r_1+r_2=2a
Elipsu tedy lze definovat pomocí středů kružnic následujícím způsobem.Definice
Mějme dány dva různé body, tj. ohniska \(E\) a \(F\), a dvě kružnice \(k_1(E, r_1)\), \(k_2(F, r_2)\), tak aby platilo \(|EF| < r_1+r_2\). Množina všech středů kružnic, které se zadanou kružnicí \(k_1\), resp. \(k_2\), mají vnitřní dotyk a s kružnicí \(k_2\), resp. \(k_1\) vnější dotyk, se nazývá elipsa; značíme ji e.
