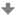Hyperbola
Poslední kuželosečkou, kterou se budeme zabývat, je hyperbola. S hyperbolou jsme se setkali již na základní škole, konkrétně při hledání grafu nepřímé úměrnosti. Na střední škole se potom rozšiřuje nepřímá úměrnost v lineární lomenou funkci, která má předpis
f:y=\frac{ax+b}{cx+d},
kde \(a\), \(b\), \(c\), \(d\) jsou reálná čísla, \(c \ne 0\) a \(ad-bc \ne 0\).
Mějme například funkci danou předpisem \(f:y=\frac{2x+3}{x+1}\). Předpis lze upravit na tvar \(f:y=2+\frac{1}{x+1}\), ze kterého lze určit souřadnice středu hyperboly. Graf dané funkce tedy vypadá následujícím způsobem, viz obr. 4.15.
Obrázek 4.15: Graf lineární lomené funkce \(f\)
Více o lineární lomené funkci na webu [2] v tématu věnujícím se Lineární lomené funkci.
Připomeňme definici hyperboly, kterou známe z [12] analytické geometrie, jako množinu bodů definovanou pomocí pojmu vzdálenost.
Definice
Mějme dány body \(E\) a \(F\), pro které platí \(|EF|>2a\). Množina všech bodů, které mají od bodů \(E\) a \(F\) absolutní hodnotu rozdílu vzdáleností rovnu \(2a\), se nazývá hyperbola; značíme ji h.
Symbolicky výše uvedenou definici zapisujeme h=\{X\in E_2; ||XE|-|XF||=2a\}. Konstanta \(a\) je délka hlavní poloosy.
Obrázek 4.16: Hyperbola a její vlastnosti
Na obr. 4.16 a 4.17 jsou zobrazeny důležité charakteristiky hyperboly:
- bod \(S\): střed hyperboly,
- přímka \(EF\): hlavní osa hyperboly \(o_1\),
- body \(A, B\) hyperboly ležící na přímce \(EF\): hlavní vrcholy hyperboly,
- přímka kolmá k hlavní ose procházející středem: vedlejší osa elipsy \(o_2\),
- úsečka spojující ohnisko hyperboly a střed, tj. \(ES, FS\): excentricita, výstřednost,
- přímky \(a_1, a_2\): asymptoty hyperboly,
- úsečka spojující hlavní vrchol hyperboly a střed, tj. \(AS, BS\): hlavní poloosa,
- úsečka spojující bod \(E'\) a bod \(A\), tj. \(E'A\): vedlejší poloosa.
Z obr. 4.17 je také vidět, že mezi velikostmi poloos a excentricitou platí z Pýthagorovy věty rovnost \(e^2=a^2+b^2\) a že hyperbola je středově souměrná podle bodu \(S\).
Obrázek 4.17: Hyperbola
Na obr. 4.17 je vidět několik vlastností hyperboly.
- hyperbola má dvě navzájem kolmé osy souměrnosti \(o_1\) a \(o_2\),
- asymptoty \(a_1\) a \(a_2\) nemusí být vždy navzájem kolmé,
- hyperbola je osově souměrná podle os úhlů, které svírají asymptoty,
- hyperbola je složena ze dvou částí, kterým říkáme větve hyperboly,
- střed \(S\) je středem úsečky \(EF\),
Co by se stalo, kdyby ohniska \(E\) a \(F\) nebyla různá? 
Příklad 4.4.1
V appletu na obr. 4.18 je zobrazena hlavní poloosa hyperboly, hlavní vrcholy \(A\) a \(B\) a ohniska \(E\) a \(F\). Bod \(X_1\), resp. \(X_2\), je průsečíkem kružnic \(k_1\) a \(k_2\) tak, aby \(k_1(E, |AR|)\) a \(k_2(F, |BR|)\). Bod \(R\) leží na přímce \(EF\) a lze s ním pohybovat. Při pohybu bodem \(R\) se vykresluje stopa bodu \(X_1\), resp. \(X_2\). Kružnice \(k_1\) a \(k_2\) se protnou pouze, pokud se bod \(R\) nachází vně úsečky \(EF\). Na základě appletu ověřte, že sestrojená množina bodů je skutečně hyperbola.
Obrázek 4.18: Applet - konstrukce hyperboly
Zamyslíme se nad tím, zda sestrojená množina bodů je skutečně hyperbola. Bod \(X_1\) má od ohniska \(E\) vzdálenost rovnou poloměru kružnice \(k_1\) a od ohniska \(F\) vzdálenost rovnou poloměru kružnice \(k_2\), tj. \(|X_1E|=|AR|\) a \(|X_1F|=|BR|\). Bod \(R\) musí ležet vně úsečky \(EF\). Leží-li bod \(R\) na opačné polopřímce k polopřímce \(EA\), lze vyjádřit poloměr kružnice \(k_1\) jako součet
|AR|=|AE|+|ER|.
A poloměr kružnice \(k_2\) jako součet
|BR|=|BS|+|SA|+|AE|+|ER|.
Rozdíl je tedy roven
|BR|-|AR|=|BS|+|SA|+|AE|+|ER|-(|AE|+|ER|)=|BS|+|SA|=|AB|.
Již však víme, že vzdálenost bodů \(A\) a \(B\) můžeme označit \(2a\) a dostáváme tedy výsledek
|BR|-|AR|=2a.
Stejné vztahy platí pro bod \(X_2\). Pokud by se bod \(R\) ležel na polopřímce opačné k polopřímce \(FB\), výpočet by probíhal analogicky. Vzniklý útvar tedy je hyperbola, tedy platí absolutní hodnota rozdílu \(||XE|-|XF||=2a\).
Hyperbola jako množina středů kružnic
Následující text byl inspirován publikací [7].
V předchozí kapitole Elipsa jsme se mimo jiné zabývali elipsou jako množinou středů kružnic dané vlastnosti. Pro nalezení takové množiny jsme měli zadána dvě ohniska \(E\) a \(F\), a dvě kružnice \(k_1(E, r_1)\), \(k_2(F, r_2)\), tak aby platilo \(|EF| < r_1+r_2\).
Elipsa je potom množina středů takových kružnic, které mají s jednou z kružnic \(k_1\) a \(k_2\) vnitřní dotyk a s druhou dotyk vnější. Nyní se budeme obdobným způsobem zabývat hyperbolou a uvidíme, že nejde o úlohu významně obtížnější.
Příklad 4.4.2
V appletu na obr. 4.19 jsou dány dva různé body \(E\) a \(F\), a dvě kružnice \(k_1(E, r_1)\), \(k_2(F, r_2)\) tak, jak tomu bylo u elipsy. Kružnice \(k\) je konstruována tak, aby s jednou z kružnic \(k_1\) a \(k_2\) vnitřní dotyk a s druhou dotyk vnější.
Pohybujte bodem \(A\) po kružnici \(k_2\) a pozorujte, jaký útvar vykreslí střed kružnice \(k\). Dále pohybujte body \(K_1\), \(K_2\) a \(F\) (tj. měňte polohu a poloměry kružnic) a zkoumejte, kdy středy kružnice \(k\) (při pohybu bodem \(A\) po kružnici \(k_2\)) začnou vykreslovat hyperbolu. Co musí platit pro poloměry kružnic \(r_1\) a \(r_2\), aby hledanou množinou středů byla hyperbola? Zaškrtávacím políčkem lze zobrazit, jakým způsobem byl bod \(X\) zkonstruován.
Obrázek 4.19: Applet - hyperbola jako množina středů kružnic
Hyperbola s ohnisky \(E, F\) vznikne, pokud kružnice \(k_1\) a \(k_2\) nemají žádný společný bod nebo pokud mají jeden společný bod a zároveň jedna z kružnic není uvnitř druhé kružnice. Pro poloměry tedy musí platit \(r_1+r_2 \leq |EF|\).
Dokažme nyní, že skutečně uvedeným způsobem vznikne hyperbola. Na obr. 4.20 jsou zobrazeny dva středy \(S_1, S_2\) kružnic, které mají s kružnicemi \(k_1\) a \(k_2\) vnější nebo vnitřní dotyk, každý na jedné větvi hyperboly.
Obrázek 4.20: Hyperbola jako množina středů kružnic
Zaměříme se nyní na bod \(S_1\). Vyjádříme absolutní hodnotu rozdílu vzdáleností bodu \(S_1\) od ohnisek hyperboly, tj. \(||ES_1|-|FS_1||\). Označíme-li poloměr hledané kružnice se středem \(S_1\) písmenem \(d_1\), můžeme vzdálenost \(|ES_1|\) vyjádřit jako \(d_1-r_1\). Obdobně \(|FS_1|\) lze vyjádřit jako \(d_1+r_2\). Tedy
||ES_1|-|FS_1||=|d_1-r_1-(d_1+r_2)|=|-r_1-r_2|=r_1+r_2.
Využili jsme toho, že poloměry kružnic \(r_1\) a \(r_2\) jsou nezáporná čísla. Součet \(r_1+r_2\) je konstantní, musí tedy platit
2a=r_1+r_2 \Rightarrow a=\frac{1}{2}(r_1+r_2).
Obdobným způsobem lze postupovat pro bod \(S_2\) na druhé větvi hyperboly. Označíme-li poloměr hledané kružnice se středem \(S_2\) písmenem \(d_2\), můžeme psát
||ES_2|-|FS_2||=|r_1+d_2-(d_2-r_2)|=|r_1+r_2|=r_1+r_2.
2a=r_1+r_2 \Rightarrow a=\frac{1}{2}(r_1+r_2).
Hyperbolu pak pomocí středů kružnic lze definovat následujícím způsobem.
Definice
Mějme dány dva různé body, ohniska \(E\) a \(F\), a dvě kružnice \(k_1(E, r_1)\), \(k_2(F, r_2)\) tak, aby platilo \(r_1+r_2 \leq |EF|\). Množina všech středů kružnic, které se zadanou kružnicí \(k_1\), resp. \(k_2\), mají vnitřní dotyk a s kružnicí \(k_2\), resp. \(k_1\), vnější dotyk, se nazývá hyperbola; značíme ji h.