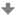Kružnice a kruh
Nejjednodušší příklad množiny bodů dané vlastnosti je kružnice. Naším úkolem tedy bude si připomenout, jak vzniká množina bodů, které mají od daného bodu stejnou vzdálenost.
Příklad 2.1.1
V appletu na obr. 2.1 je zobrazen bod \(S\) a bod \(X\), který je od bodu \(S\) vzdálen o kladnou délku \(r\). Pohybujte bodem \(X\) nebo zapněte animaci v levém dolním rohu appletu. Zkoumejte, jaké vlastnosti má výsledná množina vykreslená bodem \(X\).
Obrázek 2.1: Applet - vykreslení kružnice
Z appletu 2.1 vidíme, že množinou bodů dané vlastnosti je kružnice. Toto pozorování nyní dokážeme.
Každý bod, který do množiny patří, má od bodu \(S\) stejnou vzdálenost, kterou označíme \(r\). Všechny ostatní body, tj. body, které mají od bodu \(S\) vzdálenost větší nebo menší, do množiny nepatří.
Jak je uvedeno v kapitole Množiny bodů dané vlastnosti, musíme nyní dokázat následující dvě podmínky
- všechny body, které do množiny patří, mají od bodu \(S\) stejnou vzdálenost \(r\),
- každý bod, který do množiny nepatří, nemá od bodu \(S\) vzdálenost \(r\).
Obrázek 2.2: Kružnice - ilustrace ke zdůvodnění
1. Body \(X_1\) a \(X_2\) na obr. 2.2 mají od bodu \(S\) vzdálenost \(r\), patří tedy do dané množiny.
2. Oproti tomu bod \(Y_1\) má od bodu \(S\) vzdálenost menší než \(r\) a bod \(Y_2\) má od bodu \(S\) vzdálenost větší než \(r\), proto ani jeden do množiny nepatří.
Pomocí výše ověřených vlastností tedy můžeme formulovat definici zkoumané množiny.
Definice
Množina všech bodů v rovině, které mají od daného bodu \(S\) stejnou vzdálenost r>0, se nazývá kružnice \(k\) se středem \(S\) a poloměrem \(r\); značíme ji k(S, r).
Symbolicky výše uvedenou definici zapisujeme k=\{X\in E_2; |XS|=r\}.
Nyní se zamyslíme nad bodem \(Y_1\) na obr. 2.2. Jistě znáte množinu bodů, do které bod \(Y_1\) patří, viz obr. 2.3. O jakou množinu se jedná? 
Definice
Množina všech bodů v rovině, které mají od daného bodu \(S\) vzdálenost stejnou nebo menší než r>0, se nazývá kruh \(K\) se středem \(S\) a poloměrem \(r\); značíme ho K(S, r).
Symbolicky výše uvedenou definici zapisujeme K=\{X\in E_2; |XS| \leq r\}.
Obrázek 2.3: Kruh - ilustrace ke zdůvodnění
V příkladu 2.1.2 si připomeneme další významnou kružnici, kterou známe ze základní školy.
Příklad 2.1.2
V appletu na obr. 2.4 je zobrazen pravoúhlý \(\triangle ABX\) s pravým úhlem u vrcholu \(X\). Pohybujte bodem \(D\) nebo zapněte animaci v levém dolním rohu appletu a zjistěte, jakou množinu tvoří body \(X\).
Obrázek 2.4: Applet - vykreslení Thaletovy kružnice
Nepřekvapí nás, že se jedná o kružnici s průměrem \(AB\). Zvláštní pozornost však musíme věnovat bodům \(A\) a \(B\). Pokud by bod \(X\) byl totožný s bodem \(A\), nebo \(B\), trojúhelník \(ABX\) by neexistoval, proto tyto dva body do množiny nepatří.
Nyní musíme dokázat, že se skutečně jedná o kružnici s průměrem \(AB\) bez bodů \(A, B\). Z předchozí kapitoly víme, že důkaz bude obsahovat dvě části, a to:
- každý bod \(X\) z dané množiny je vrcholem pravoúhlého trojúhelníku \(ABX\) s pravým úhlem u vrcholu \(X\),
- bod, který není obsažen v dané množině, není vrcholem pravoúhlého trojúhelníku \(ABX\) s pravým úhlem u vrcholu \(X\).
1. K první části důkazu jsou v obr. 2.5 vyznačeny úhly \(\alpha\) a \(\beta\). Z definice kružnice pro libovolný bod \(X\) na kružnici \(k\) platí, že \(|AS|=|SB|=|SX|\), a proto jsou \(\triangle ASX\) a \(\triangle SBX\) rovnoramenné. Z toho plyne, že \(|∡ SAX|=|∡ AXS|=\alpha\) a \(|∡ SBX|=|∡ BXS|=\beta\). (Je zřejmé, že bod \(X\) nemůže být totožný s bodem \(A\) nebo \(B\), jelikož by trojúhelník neexistoval.)
Obrázek 2.5: Kružnice s vyznačenými úhly \(\alpha, \beta\)
Z vlastností každého trojúhelníku víme, že součet velikostí vnitřních úhlů trojúhelníku je \(180°\), tedy
|∡ AXB|+|∡ XBA|+|∡ BAX|=180°.
Velikost úhlu u vrcholu \(X\) lze vyjádřit jako \(|∡ AXB|=|∡ AXS|+|∡ BXS|\). Dostaneme tedy rovnost
\alpha + \beta + \alpha + \beta = 180°,
kterou lze upravit na \(\alpha + \beta = 90°\). Úhel u vrcholu \(X\) je tedy pravý.
2. Zbývá dokázat druhou část, tedy že pro každý bod \(Y\), který na kružnici neleží, úhel \(AYB\) není pravý. Dle polohy bodu \(Y\) vůči kružnici \(k\) dostaneme dvě situace zobrazené na následujícím obr. 2.6.
Obrázek 2.6: Kružnice - různé polohy bodu \(Y\)
Může nastat situace, kdy bod \(Y\), \(Y=Y_1\), leží na odvěsně \(XB\). (Zvolíme-li bod \(Y_1\) libovolně uvnitř kružnice \(k\), pak existuje bod \(X\) takový, že \(Y_1\) leží na odvěsně \(XB\).) Z předchozí části důkazu víme, že \(|∡ AXB|=90°\) a \(\triangle AXY_1\) je pravoúhlý, proto úhel \(AY_1X\) musí být ostrý (plyne ze součtu velikostí vnitřních úhlů v trojúhelníku) a úhel k němu vedlejší, tj. \(∡ AY_1B\), musí být tupý.
Dále může nastat situace, kdy bod \(Y\), \(Y=Y_2\), je vnějším bodem kružnice \(k\). Opět platí, že \(|∡ AXB|=90°\), a jelikož trojúhelník \(AXY_2\) je pravoúhlý s pravým úhlem u \(X\), musí být \(∡ AY_2B\) ostrý. Zde jsme uvažovali takový bod \(Y_2\), který leží na \(\mapsto BX\). Stejně tak by mohl ležet na \(\mapsto AX\), důkaz by však probíhal obdobným způsobem.
Definice
Množina všech vrcholů \(X\) pravoúhlých trojúhelníků \(ABX\) s přeponou \(AB\) v rovině se nazývá Thaletova kružnice nad průměrem \(AB\); značíme ji \(\tau_{AB}\).
Symbolicky výše uvedenou definici zapisujeme \tau_{AB}=\{X\in E_2; |∡ AXB|=90° \}, viz obr. 2.7.
Obrázek 2.7: Thaletova kružnice