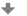Vzdálenost geometrických útvarů
Pro lepší porozumění dalšímu textu si zopakujeme vybrané důležité pojmy. Nejjednodušší pojem, se kterým pracujeme spíše intuitivně, je vzdálenost dvou bodů \(A, B\), kterou rozumíme délku (velikost) úsečky \(AB\), symbolicky zapisujeme \(|AB|\). (Vzdálenost dvou totožných bodů je potom 0.)
Vzdáleností dalších útvarů v rovině je potom nejmenší ze všech vzdáleností bodů \(A\) a \(B\), kde bod \(A\) je libovolným bodem jednoho útvaru a bod \(B\) libovolným bodem druhého útvaru. Jinými slovy můžeme říci, že vzdálenost dvou útvarů je velikost nejkratší úsečky, která tato dva útvary spojuje. Z těchto dvou poznatků lze odvodit konkrétní případy.
Pomocí vzdálenosti dvou bodů můžeme zavést vzdálenost bodu od přímky, značíme \(|pX|\). Nejkratší vzdálenost bodu \(X\) od přímky \(p\) je rovna vzdálenosti bodu \(X\) a jeho kolmého průmětu \(X'\) na přímku \(p\), viz obr. 1.1. 
Obrázek 1.1: Vzdálenost bodu od přímky
Dalším pojmem odvozeným ze vzdálenosti bodu od přímky je vzdálenost bodu od úsečky, značíme \(|AB,X|\). Mějme bod \(X\) a úsečku \(AB\). Pokud bychom postupovali stejně jako u vzdálenosti bodu od přímky, kolmý průmět bodu \(X\) by nemusel vždy ležet na úsečce \(AB\), ale na přímce \(AB\), viz obr. 1.2.
Obrázek 1.2: Vzdálenost bodu od úsečky
Na obr. 1.2 vidíme, že bod \(X_1'\) je kolmý průmět bodu \(X_1\) na přímku \(AB\). Bod \(X_1'\) ale neleží na úsečce \(AB\), proto vzdálenost úsečky \(AB\) a bodu \(X_1\) nemůže být délka úsečky \(X_1X_1'\). Vzdálenost dvou útvarů je délka nejkratší úsečky spojující dva útvary, proto vzdálenost bodu \(X_1\) od úsečky \(AB\) musí být jedině délka úsečky \(X_1A\). Obdobně vzdálenost bodu \(X_3\) a úsečky \(AB\) je délka úsečky \(X_3B\) a vzdálenost bodu \(X_2\) od úsečky \(AB\) je potom vzdálenost bodu \(X_2\) a jeho kolmého průmětu \(X_2'\).
Nyní nám zbývá určit vzdálenost bodu od polopřímky, značíme \(|\mapsto AB,X|\). Na obr. 1.3 je zobrazena polopřímka \(AB\) a body \(X_1\) a \(X_2\). Obdobně jako u úsečky je vzdálenost bodu \(X_1\) od polopřímky \(AB\) rovna délce úsečky \(X_1A\) a vzdálenost bodu \(X_2\) od polopřímky \(AB\) je vzdálenost bodu \(X_2\) a jeho kolmého průmětu \(X_2'\) na polopřímku \(AB\).
Obrázek 1.3: Vzdálenost bodu od polopřímky
Poslední pojem, který si rozebereme, je vzdálenost bodu od kružnice. Na obr. 1.4 je zobrazena kružnice \(k\) se středem \(S\) a poloměrem \(r\) a body \(X_1, X_2\) a \(X_3\).
Obrázek 1.4: Vzdálenost bodu od kružnice
Bod \(X_1\) je vnitřním bodem kružnice \(k\). Nejkratší úsečka spojující kružnici \(k\) a bod \(X_1\) bude ležet na poloměru kružnice \(k\). Průsečík uvedeného poloměru a kružnice \(k\) je na obr. 1.4 označen \(X_1'\). Vzdálenost bodu \(X_1\) od kružnice \(k\) je potom délka úsečky \(X_1X_1'\).
Bod \(X_2\) je vnějším bodem kružnice \(k\). Průsečík úsečky \(X_2S\) s kružnicí \(k\) označíme \(X_2'\). Z obrázku 1.4 vidíme, že vzdálenost bodu \(X_2\) od kružnice \(k\) je rovna délce úsečky \(X_2X_2'\).
Obecně lze říci, že vzdálenost bodu od kružnice je rovna absolutní hodnotě rozdílu délky úsečky \(XS\) a poloměru kružnice \(r\), tj. \(||XS|-r|\). Tento vztah platí i pro bod \(X_3\), který je bodem kružnice \(k\).
Dále bychom mohli rozebrat vzdálenosti dalších útvarů (např. vzdálenost přímky od kružnice), všechny však vychází z výše uvedených pojmů. Stačí pouze nalézt nejkratší úsečku spojující dané útvary (např. v případě přímky a kružnice by se jednalo o kolmici k přímce procházející středem kružnice).