Kuželosečky jako množiny středů kružnic
Dalšími množinami bodů, kterými se budeme zabývat, jsou kuželosečky. Na střední škole jste se zabývali zejména kuželosečkami regulárními, tedy parabolou, hyperbolou, kružnicí a elipsou, a to zejména z pohledu analytické geometrie. Zaměříme se pouze na regulární kuželosečky z pohledu planimetrie. Zopakujeme základní vlastnosti kuželoseček a následně zavedeme kuželosečky jako množiny středů kružnic dané vlastnosti.
Následující kapitoly věnující se parabole, elipse a hyperbole tedy vychází z předpokladu, že studenti ze střední školy znají základní pojmy, které s danými kuželosečkami souvisí. Pojmy tedy nejsou kompletně zavedeny a odvozeny, pouze zopakovány.
Kuželosečky vzniknou řezem rotační kuželové plochy. Kuželovou plochu si jednoduše můžeme představit jako plášť nekonečně vysokého dvojkužele (tj. dva shodné kužely spojené vrcholem, viz obr. 4.1). Povedeme-li potom příslušný řez kuželové plochy rovinou, získáme jednu z kuželoseček - parabola, hyperbola, elipsa (případně kružnice, které jsme se věnovali v kapitole Kružnice a kruh).
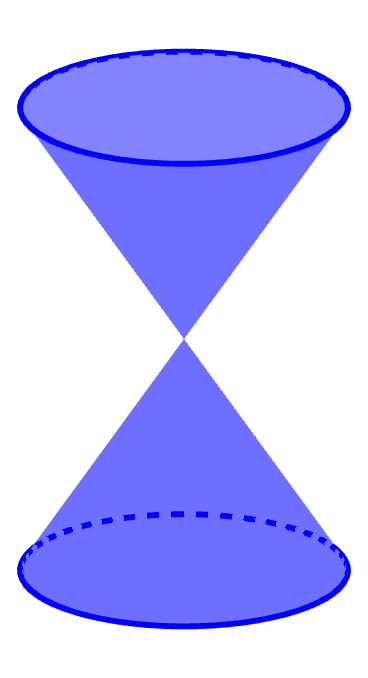
Obrázek 4.1: Dvojkužel
Příklad 4.1.1
V následujícím appletu na obr. 4.2 je zobrazena část kuželové plochy a roviny \(\sigma\) a \(\rho\). Rovina \(\sigma\) je kolmá k ose kuželové plochy. Pohybujte bodem \(A\) pro změnu odchylky rovin \(\sigma\) a \(\rho\) a bodem \(B\) pro změnu pozice roviny \(\rho\). Jak budou vypadat jednotlivé křivky, které vzniknou jako řez kuželové plochy rovinou \(\rho\)?
Obrázek 4.2: Applet - řez kuželem
Mohou nastat celkem tři situace. Je-li- \(\alpha<\beta\), vznikne uzavřená křivka podobná kružnici - elipsa,
- \(\alpha=\beta\), vznikne neuzavřená křivka na jedné části kuželové plochy - parabola,
- \(\alpha>\beta\), vznikne neuzavřená křivka na obou částech kuželové plochy - hyperbola.
Všimněte si také, že čím více se velikost úhlu \(\alpha\) přibližuje \(0°\), tím více se elipsa podobá kružnici. Tuto skutečnost více okomentujeme v kapitole věnující se Elipse. Uvedené poznatky shrnuje obr. 4.3, na kterém jsou schematicky zachyceny tři situace řezu kuželové plochy rovinou dle vztahů mezi velikostmi úhlů \(\alpha\) a \(\beta\).
Obrázek 4.3: Druhy kuželoseček
Vraťme se nyní k appletu na obr. 4.2. Kromě uvedených regulárních kuželoseček (elipsa, parabola, hyperbola, kružnice) mohou nastat další speciální případy - pokud rovina řezu prochází vrcholem kuželu. Takovým kuželosečkám se říká singulární a jedná se o
- bod: rovina řezu prochází pouze vrcholem a zároveň \(\alpha<\beta\),
- přímka: rovina řezu prochází vrcholem a zároveň \(\alpha=\beta\),
- dvě různoběžné přímky: rovina řezu prochází vrcholem a zároveň \(\alpha>\beta\).
Na kuželové ploše nelze řezem získat další singulární kuželosečku, a to dvě rovnoběžné přímky. Ty vzniknou na válcové ploše při řezu rovinou rovnoběžnou s osou válcové plochy.