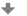Osa mezikruží
Mějme dány dvě soustředné kružnice \(k_1(S, r_1)\) a \(k_2(S, r_2)\), kde r_1 \lt r_2. Nyní budeme hledat takovou množinu bodů, které mají od obou kružnic stejnou vzdálenost. Využijeme při tom znalost pojmu vzdálenost bodu od kružnice.
Hledejme nyní bod \(X\) tak, aby měly od obou kružnic \(k_1\) a \(k_2\) stejnou vzdálenost. Je přitom zřejmé, že hledané body \(X\) budou ležet v mezikruží vymezeném kružnicemi \(k_1\) a \(k_2\). Zvolíme-li na kružnici \(k_2\) libovolný bod \(A\) a sestrojíme poloměr \(AS\), pak bod \(B\) je průsečíkem poloměru \(AS\) a kružnice \(k_1\). Je zřejmé, že střed úsečky \(AB\) splňuje požadovanou vlastnost, viz obr. 2.23.
Obrázek 2.23: Konstrukce bodu \(X\)
Příklad 2.5.1
Na appletu na obr. 2.24 jsou zobrazeny dvě soustředné kružnice \(k_1, k_2\) se středem \(S\) a bod \(X\), který je středem úsečky \(AB\), kde \(A \in k_1\) a \(B \in k_2\). Bod \(X\) má stejnou vzdálenost od obou kružnic. V appletu pohybujte bodem \(A\) nebo zapněte animaci v levém dolním rohu appletu. Jakou množinu bodů vykreslí polohy středů úsečky \(AB\) při změně polohy bodu \(A\) na \(k_2\)?
Obrázek 2.24: Applet - osa mezikruží
Z appletu na obr. 2.24 vidíme, že vznikne kružnice se středem v bodě \(S\). Poloměr hledané kružnice je vzdálenost bodů \(S\) a \(X\), kterou lze vyjádřit jako
|SX|=r_1+\frac{1}{2}|AB|=r_1+\frac{1}{2}(r_2-r_1)=\frac{1}{2}(r_1+r_2).
Zjištěný poznatek dokážeme, nalezenou množinu bodů označíme \(o\), viz obr. 2.25.
Obrázek 2.25: Osa \(o\) mezikruží s vyznačenými body \(X\), \(Y_1\), \(Y_2\), \(Y_3\)
1. Nyní ověříme, že každý bod nalezené kružnice má požadovanou vlastnost, tj. má od obou kružnic stejnou vzdálenost. Z definice vzdálenosti bodu od kružnice víme, že vzdálenost bodu \(X\) od kružnice \(k_1\) je \(|BX|\) a vzdálenost bodu \(X\) od kružnice \(k_2\) je \(|AX|\). Zároveň nalezená kružnice má střed \(S\) a poloměr \(\frac{1}{2}(r_1+r_2)\). Lze tedy rozepsat
|Xk_1|=|AX|=|SX|-r_1=\frac{1}{2}(r_1+r_2)-r_1=\frac{1}{2}(r_2-r_1),
|Xk_2|=|BX|=r_2-|SX|=r_2-\frac{1}{2}(r_1+r_2)=\frac{1}{2}(r_2-r_1).
Uvedené vztahy jsou shodné, tedy kružnice \(o\) má od obou zadaných kružnic stejnou vzdálenost.
2. Ukážeme, že každý bod \(Y\), který má danou vlastnost, musí ležet na kružnici \(o\) se středem \(S\) a poloměrem \(\frac{r_1 + r_2}{2}\). Předpokládejme tedy, že \(|Yk_1|=|Yk_2|\) (v obr. 2.25 jsou body \(Y\) zobrazeny pouze ilustračně, neodpovídají tedy vzdálenosti od kružnic \(k_1\), \(k_2\)). Leží-li bod \(Y\) v mezikruží určeném kružnicemi \(k_1\) a \(k_2\), tj. \(Y=Y_1\), lze vzdálenost bodu \(Y_1\) od kružnice \(k_1\) vyjádřit jako \(r_2-r_1-|Y_1k_2|\). Dostaneme tedy rovnici
r_2-r_1-|Y_1k_2|=|Y_1k_2|,
ze které po úpravě dostaneme
|Y_1k_2|=\frac{1}{2}(r_2-r_1).
Vzdálenost bodu \(Y_1\) od kružnice \(k_2\) je tedy rovna polovině \(|AB|\), což odpovídá bodům na kružnice se středem \(S\) a poloměrem \(\frac{r_1 + r_2}{2}\). Z obr. 2.25 je zřejmé, že body \(Y\), které leží vně mezikruží (např. bod \(Y=Y_2\), či \(Y=Y_3\)), nemohou mít stejnou vzdálenost od obou kružnic. Lze tedy formulovat definici.
Definice
Množinu všech bodů v rovině, které mají od daných kružnic \(k_1(S,r_1)\) a \(k_2(S,r_2)\), \(r_1 \neq r_2\), stejnou vzdálenosti nazveme osou mezikruží; značíme ji o (S, \frac{r_1 + r_2}{2}).
Symbolicky danou množinu bodů zapisujeme o (S, \frac{r_1 + r_2}{2})=\{X\in E_2; |Xk_1|=|Xk_2|\}.
Poznamenejme, že pokud by se rovnaly poloměry kružnic \(r_1\) a \(r_2\), vznikla by jediná kružnice, tudíž nelze hovořit o ose mezikruží.
Ekvidistanta kružnice
Obdobně jako v předchozí kapitole zabývající se osou rovinného pásu, i v případě osy mezikruží lze hledet množinu všech bodů, které mají stejnou vzdálenost \(d\) od dané kružnice \(k\), tj. ekvidistantu kružnice.
Příklad 2.5.2
Na následujícím appletu na obr. 2.26 je zobrazena kružnice \(k\) se středem \(S\) a poloměrem \(r\), bod \(K\), který leží na kružnici \(k\), a kružnice \(m\) se středem \(K\) a poloměrem \(d\). Pohybujte bodem \(K\) po kružnici \(k\) a zkoumejte, jaký vznikne útvar, aby platilo \(|Xk|=d\). Pomocí posuvníku měňte poloměr \(r\) a vzdálenost \(d\) a pozorujte, jak se bude výsledný útvar měnit při změnách \(r\) a \(d\).
Obrázek 2.26: Applet - ekvidistanta kružnice
Z appletu na obr. 2.26 jsme zjistili, že mohou nastat celkem tři situace, viz obr. 2.27. V závislosti na vzdálenosti \(d\) je ekvidistantou kružnice:
- pro r \lt d je to jedna kružnice \(e_1(S, r+d)\),
- pro r = d je to jedna kružnice \(e_1(S, 2r)\) a bod \(S\),
- pro \(r>d\) jsou to dvě kružnice \(e_1(S, r+d)\) a \(e_2(S, r-d)\).
Zdůvodnění všech tří situací by probíhala obdobně jakou u osy mezikruží, a to s využitím poloměrů \(r\) a \(d\).
Definice
Množinu všech bodů v rovině, které mají od dané kružnice \(k(S,r)\) danou vzdálenost \(d>0\), nazveme ekvidistantou kružnice \(k\); značíme ji \(e_1\), resp. \(e_2\).
Symbolicky výše uvedenou definici zapisujeme e_1 \cup e_2 =\{X\in E_2; |Xk|=d\}.
Obrázek 2.27: Ekvidistanta kružnice \(k\)
V předchozí kapitole jsme se věnovali ekvidistantě úsečky neboli oválu. Nyní hledejme množinu bodů, která má od dvou oválů stejnou vzdálenost, tj. osu oválu.
Příklad 2.5.3
Na následujícím appletu na obr. 2.28 jsou zobrazeny dva ovály \(e_1\) a \(e_2\), které vznikly jako ekvidistanty stejné úsečky \(AB\). Pomocí šipek v levém dolním rohu si zobrazte jednotlivé kroky řešení úlohy a pozorujte, jaký útvar bude osou oválů \(e_1\) a \(e_2\). Vysvětlete.
Obrázek 2.28: Applet - osa oválů
V appletu na obr. 2.28 jsou jako první sestrojeny přímky \(p_1\) a \(p_2\). Přímky vznikly jako osy pásů daného přímkami \(a_1\) a \(a_2\), resp. \(a_3\) a \(a_4\), na kterých leží části oválů. Následně jsou sestrojeny osy mezikruží kružnic, které tvoří „boční části“ oválu. V posledním kroku je sestrojena osa \(o\) oválů \(e_1\) a \(e_2\), která je také oválem.