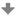Převod mezi jednotlivými vyjádřeními
Různé možnosti zadání stejné posloupnosti vyžadují možnost převodu jednoho vyjádření na druhé.
Některé jsou velice jednoduché, ...
výčet hodnot \(\longrightarrow\) graf
graf \(\longrightarrow\) výčet hodnot
vzorec pro \(n\)-tý člen \(\longrightarrow\) výčet hodnot
rekurentní vzorec \(\longrightarrow\) výčet hodnot
... některé jsou o něco méně jednoduché ...
výčet hodnot (graf) \(\longrightarrow\) vzorec pro \(n\)-tý člen
výčet hodnot (graf) \(\longrightarrow\) rekurentní vzorec
V těchto případech je potřeba závislost odhadnout. Pokud je však nekonečná posloupnost zadaná výčtem hodnot, je potřeba, jak již bylo řečeno, aby závislost byla na první pohled vidět.
... a některé se mohou zdát na první pohled složitější.
vzorec pro \(n\)-tý člen \(\longrightarrow\) rekurentní vzorec
Pokud chceme převést vzorec pro \(n\)-tý člen na rekurentní vzorec, můžeme na to jít více způsoby. Zde platí, že více způsobů většinou vede na více řešení. Rekurentních vzorců pro jednu posloupnost je mnoho, na konci si stačí jen vybrat.
Mnohdy nejjednodušší způsob je řešení opět pouze odhadnout. Většinou stačí si vypsat pár prvních členů a rekurentní závislost je na světě. Pokud však ani po dlouhém zkoumání nic nevidíte, nepropadejte panice, existují i prozaičtější způsoby řešení. Mnohé řekne zkoumání podílu (případně rozdílu) sousedních dvou členů.
\(a_n = n^2 + 1 \longrightarrow \{2, 5, 10, 17, \ldots, n^2 + 1, {(n+1)}^2 + 1, \ldots\}\)
odhad:
\(a_{n+1} = a_n + (2n + 1)\), \(a_1 = 2\)
rozdíl sousedních členů: \(a_{n+1} - a_n\)
\(a_{n+1} - a_n = [(n+1)^2 + 1] - (n^2 + 1)\)
\(a_{n+1} - a_n = n^2 + 2n + 1 + 1 - n^2 - 1\)
\(a_{n+1} - a_n = 2n + 1\), a odtud
\(a_{n+1} = a_n + (2n + 1)\), \(a_1 = 2\)
podíl sousedních členů: \(a_{n+1} \over a_n\)
\({{a_{n+1}} \over {a_n}} = {{[(n+1)^2 + 1]} \over {(n^2 + 1)}}\)
\({a_{n+1} \over a_n} = {{(n^2 + 2n + 2 + 1)} \over {(n^2 + 1)}}\), a odtud
\(a_{n+1} = a_n {{n^2 + 2n + 2} \over {n^2 + 1}}\), \(a_1 = 2\)
Je vidět, že třemi různými postupy jsme získali postupně dvě různá řešení. Také je vidět, že zde bylo lepší zkoumat rozdíl než podíl. Vhodnější postup se dá určit do jisté míry už na začátku. Pokud vzorec pro \(n\)-tý člen "obsahuje násobení", je většinou lepší dělit, pokud "obsahuje pouze sčítání a odčítání", je lepší odčítat.
rekurentní vzorec \(\longrightarrow\) vzorec pro \(n\)-tý člen
I v tomto případě je nejjednodušší způsob, jak získat příslušné vyjádření, odhad. I zde je ale záchrana, pokud se nám odhadnout řešení nedaří. Postup bude nejlépe vidět na příkladě.
\(a_{n+1} = a_n + 5\), \(a_1 = 1 \longrightarrow \{1, 6, 11, 16, \ldots\}\)
odhad:
\(a_n = 5n - 4\)
jiný postup:
Vypíšeme si prvních \(n + 1\) členů, ale tentokrát trochu jinak ...
\(a_1 = 1\)
\(a_2 = a_1 + 5\)
\(a_3 = a_2 + 5\)
...
\(a_n = a_{n-1} + 5\)\(a_{n+1} = a_n + 5\)
... a tyto rovnosti sečteme ...
\(a_1 + a_2 + a_3 + \ldots + a_{n+1} = 1 + a_1 + 5 + a_2 + 5 + \ldots + a_n + 5\)
... upravíme ...
\(a_{n+1} = 1 + 5 + 5 + \ldots + 5\)
\(a_{n+1} = 1 + 5n\)
... a nakonec "posuneme" index tak, abychom získali vzorec pro \(a_n\).
\(a_n = 1 + 5(n-1)\)
Ne vždy si pomůžeme sčítáním. Někdy je lepší rovnosti vynásobit.
\(a_{n+1} = 3a_n\), \(a_1 = 1 \longrightarrow \{1, 3, 9, 27\}\)
odhad:
\(a_n = 3^{n - 1}\)
jiný postup:
Opět si vypíšeme prvních \(n + 1\) členů ...
\(a_1 = 1\)
\(a_2 = 3a_1\)
\(a_3 = 3a_2\)
...
\(a_n = 3a_{n-1}\)\(a_{n+1} = 3a_n\)
... a tyto rovnosti tentokrát vynásobíme ...
\(a_1 \cdot a_2 \cdot a_3 \cdot \ldots \cdot a_{n+1} = 1 \cdot 3a_1 \cdot 3a_2 \cdot \ldots \cdot 3a_n\)
... pokud jsou všechna \(a_i\) nenulová, upravíme ...
\(a_{n+1} = 1 \cdot 3 \cdot 3 \cdot \ldots \cdot 3\)
\(a_{n+1} = 3^n\)
... a opět "posuneme" index tak, abychom získali vzorec pro \(a_n\).
\(a_n = 3^{n - 1}\)