Posloupnosti a řady

Geometrická posloupnost

Definice

Posloupnost $(a_n)$ se nazývá geometrická právě tehdy, když

$\exists q \in R \; \forall n \in N$ platí

$a_{n+1} = a_n \cdot q$

Číslo

$q$ se nazývá kvocient aritmetické posloupnosti.

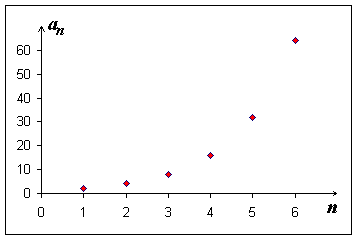
Obr. 4.2: Graf geometrické posloupnosti

Stejně jako je aritmetická posloupnost "odvozená" od lineární funkce, je geometrická posloupnost "odvozená" od exponenciální funkce tvaru

$y = k \cdot z^x$

Každou geometrickou posloupnost lze zapsat ve tvaru

$a_n = a_1 \cdot q^{n-1}$
$a_n = a_1 \cdot {1 \over q} \cdot q^n$

... a to je právě tehdy, když každý člen posloupnosti (kromě prvního) je geometrickým průměrem "svých sousedů".
$\forall n \in N - \{1\}$ platí $a_n = \sqrt{a_{n-1} \cdot a_{n+1}}$

Příklady

$\{-1, 1, -1, 1, -1, \ldots \} \longrightarrow$ kvocient

$q = -1$

$a_n = {1 \over {2^n}} \longrightarrow$ kvocient

$q = {1 \over 2}$ Zobrazit řešení

$a_n = {1 \over {2^n}}$
$a_{n+1} = {1 \over {2^{n+1}}}$
${a_{n+1} \over a_n} = {1 \over {2^{n+1}}} \cdot {2^n \over 1} = {1 \over 2}$
Podíl každých dvou sousedních členů je $1 \over 2$

$a_n = 4a_{n-1}$ ,

$a_1 = 1 \longrightarrow$ kvocient

$q = 4$

Vlastnosti geometrických posloupností

monotónnost

rostoucí $\Leftrightarrow a_1 \gt 0$ , $q \gt 1$ nebo $a_1 \lt 0$ , $0 \lt q \lt 1$
klesající $\Leftrightarrow a_1 \gt 0$ , $0 \lt q \lt 1$ nebo $a_1 \lt 0$ , $q \gt 1$

omezenost

shora omezená $\Leftrightarrow a_1 \lt 0$ , $q \gt 1$
zdola omezená $\Leftrightarrow a_1 \gt 0$ , $q \gt 1$
omezená $\Leftrightarrow |q| \lt 1$ nebo $|q| = 1$ nebo $a_1 = 0$

Příklady

$\{-1, 1, -1, 1, -1, \ldots \} \longrightarrow$ kvocient

$q = -1$ ,

$a_1 = -1$ , ani rostoucí, ani klesající, omezená

$a_n = {1 \over {2^n}} \longrightarrow$ kvocient

$q = {1 \over 2}$ ,

$a_1 = {1 \over 2}$ , klesající, omezená

$a_n = 4a_{n-1}$ ,

$a_1 = 1 \longrightarrow$ kvocient

$q = 4$ ,

$a_1 = 1$ , rostoucí, zdola omezená

Vztahy platící pro geometrické posloupnosti

Věta

Nechť

$(a_n)_{n=1}^{\infty}$ je geometrická posloupnost s prvním členem

$a_1$ a kvocientem

$q$ , potom platí

$a_n = a_{1} \cdot q^{n-1}$

zobraz důkaz

Důkaz matematickou indukcí:

1.

$n = 1$

$a_1 = a_{1}q^{1-1}$

2.

$n = k$

$a_k = a_{1}q^{k - 1}$

$a_{k+1} = a_{1}q^{k+1-1}$

$a_{k+1} = a_{1}q^k \longrightarrow$ k tomuto chceme dospět

z definice:

$a_{k+1} = a_{k}q$
induk. před:

$a_{k+1} = a_{1}q^{k-1}q = a_{1}q^k$

Věta

Nechť

$(a_n)_{n=1}^{\infty}$ je geometrická posloupnost s prvním členem

$a_1$ a kvocientem

$q$ , potom pro součet

$s_n$ , prvních

$n$ členů této geometrické posloupnosti platí

$s_n = na_1$ pokud

$q = 1$

$s_n = a_1 {{q^n - 1} \over {q-1}}$ pokud

$q \not = 1$

zobraz důkaz

$q = 1$

$s_n = a_1 + a_1 + a_1 + \ldots + a_1 = na_1$

2.

$q \not = 1$

$s_n = a_1 + a_2 + a_3 + \ldots + a_n$

tento součet si přepíšeme pomocí vztahu

$k$ -tého a prvního členu ...

$s_n = a_1 + (a_{1}q) + (a_{1}q^2) + (a_{1}q^3) + \ldots + (a_{1}q^{n-1})$

... rovnost vynásobíme

$q$ ...

$s_{n}q = (a_{1}q) + (a_{1}q^2) + (a_{1}q^3) + \ldots + (a_{1}q^{n-1}) + a_{1}q$

... a oba řádky odečteme ...

$s_n - s_{n}q = a_1 - (a_{1}q^n)$

... a už jen upravit ...

$s_{n} (1-q) = a_{1}(1-q^n)$

$s_n = a_{1} {{q^n - 1} \over {q - 1}}$

Geometrická posloupnost

Vlastnosti geometrických posloupností

Vztahy platící pro geometrické posloupnosti

Titulní stránka

Úvod

Definice

Zadání

Vlastnosti

Speciální posloupnosti

Limita

Řady

Rejstřík