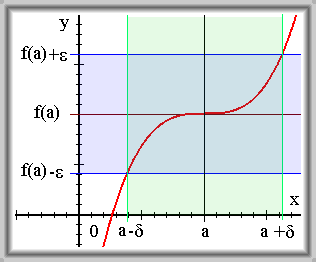
Řekneme, že funkce \(f\) je spojitá v bodě \(a\), jestliže k libovolně zvolenému okolí bodu \(f\)(\(a\)) existuje takové okolí bodu \(a\), že pro všechna \(x\) z tohoto okolí bodu \(a\) patří hodnoty \(f\)(\(x\)) do zvoleného okolí bodu \(f\)(\(a\)).
Spojitost funkce v bodě a na intervalu
Definice
Řekneme, že funkce \(f\) je spojitá v bodě \(a\), jestliže \(\forall \varepsilon \gt 0\quad \exists \delta \gt 0\quad \forall x \in \mathbb{R}\) platí \(\forall x \quad x \in \mathrm{U}(a,\,\delta) \Rightarrow f(x) \in \mathrm{U}(f(a),\,\varepsilon)\)
Poznámka

|
|

|
Definice
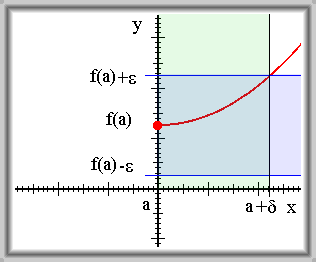
Řekneme, že funkce \(f\) je spojitá v bodě \(a\) zprava, jestliže \(\forall \varepsilon \gt 0\quad \exists \delta \gt 0\quad \forall x \in \mathbb{R}\) platí \(\forall x \quad x \in \mathrm{U}^{+}(a,\,\delta) \Rightarrow f(x) \in \mathrm{U}(f(a),\,\varepsilon)\)
Poznámka
Řekneme, že funkce \(f\) je spojitá v bodě \(a\) zprava, jestliže k libovolně zvolenému okolí bodu \(f\)(\(a\)) existuje takové pravé okolí bodu \(a\), že pro všechna \(x\) z tohoto okolí bodu \(a\) patří hodnoty \(f\)(\(x\)) do zvoleného okolí bodu \(f\)(\(a\)).

|
|

|
Definice
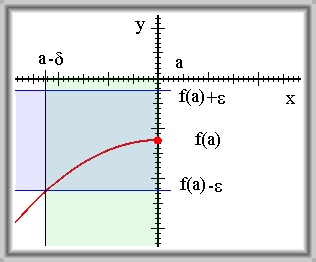
Řekneme, že funkce \(f\) je spojitá v bodě \(a\) zleva, jestliže \(\forall \varepsilon \gt 0\quad \exists \delta \gt 0\quad \forall x \in \mathbb{R}\) platí \(\forall x \quad x \in \mathrm{U}^{-}(a,\,\delta) \Rightarrow f(x) \in \mathrm{U}(f(a),\,\varepsilon)\)
Poznámka
Řekneme, že funkce \(f\) je spojitá v bodě \(a\) zleva, jestliže k libovolně zvolenému okolí bodu \(f\)(\(a\)) existuje takové levé okolí bodu \(a\), že pro všechna \(x\) z tohoto okolí bodu \(a\) patří hodnoty \(f\)(\(x\)) do zvoleného okolí bodu \(f\)(\(a\)).

|
|

|
Definice
Řekneme, že funkce \(f\) je spojitá v otevřeném intervalu \((a, \,b)\), je-li spojitá v každém bodě tohoto intervalu.
Definice
Řekneme, že funkce \(f\) je spojitá v uzavřeném intervalu \(\langle a, \,b\rangle\), je-li spojitá v \((a, \,b)\) a v bodě \(a\) je spojitá zprava a v bodě \(b\) je spojitá zleva.
Několik příkladů pro lepší objasnění pojmu spojitost funkce v bodě.
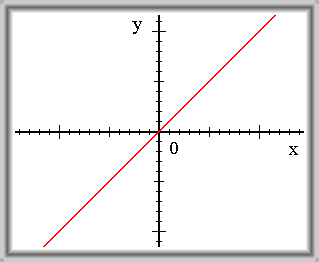
Funkce \(f(x) = x\) je spojitá v 0.
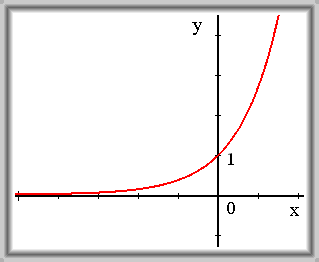
Funkce \(f(x) = e^{x}\) je spojitá v 0.
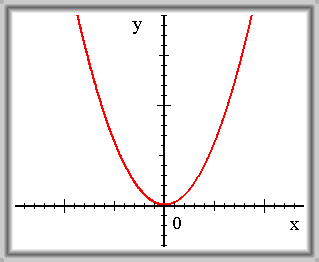
Funkce \(f(x) = x^{2}\) je spojitá v 0.
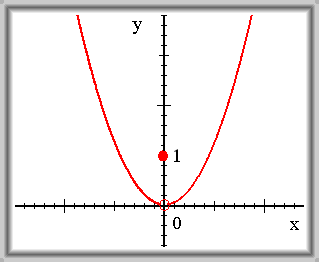
Funkce \(f(x) = \begin{cases}x^{2}&\mathrm{pro}\quad {x \in \{ \mathbb{R} \setminus {0}}\}\cr 1&\mathrm{pro}\quad{x = 0}\end{cases}\) není spojitá v 0.