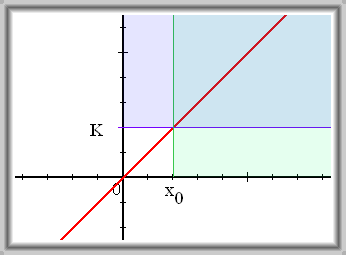
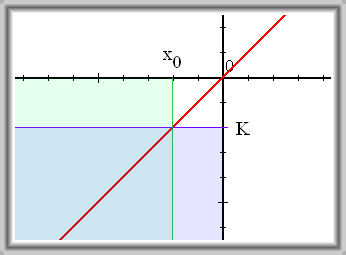
Ke každému reálnému číslu \(K\) existuje takové reálné číslo \(x_0\), že pro všechna reálná \(x \gt x_0\) platí \(f(x) \gt K\).
Nevlastní limita v nevlastním bodě
Definice
Řekneme, že funkce \(f\) má v nevlastním bodě \(+ \infty\) nevlastní limitu \(+ \infty\) právě tehdy, když
Značení: \(\lim_{x \to +\infty} f(x) = +\infty\)
Čteme: Limita funkce \(f\) pro \(x\) blížící se k \(+ \infty\) je rovna \(+ \infty\)
Poznámka

|
|

|
Definice
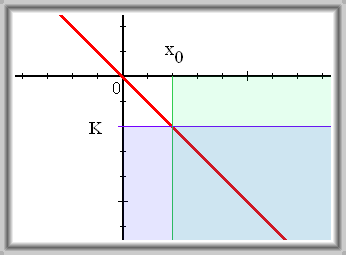
Řekneme, že funkce \(f\) má v nevlastním bodě \(+ \infty\) nevlastní limitu \(- \infty\) právě tehdy, když
Značení: \(\lim_{x \to +\infty} f(x) = -\infty\)
Čteme: Limita funkce \(f\) pro \(x\) blížící se k \(+ \infty\) je rovna \(- \infty\)
Poznámka
Ke každému reálnému číslu \(K\) existuje takové reálné číslo \(x_0\), že pro všechna reálná \(x \gt x_0\) platí \(f(x) \lt K\).

|
|

|
Definice
Řekneme, že funkce \(f\) má v nevlastním bodě \(- \infty\) nevlastní limitu \(+ \infty\) právě tehdy, když
Značení: \(\lim_{x \to -\infty} f(x) = +\infty\)
Čteme: Limita funkce \(f\) pro \(x\) blížící se k \(- \infty\) je rovna \(+ \infty\)
Poznámka
Ke každému reálnému číslu \(K\) existuje takové reálné číslo \(x_0\), že pro všechna reálná \(x \lt x_0\) platí \(f(x) \gt K\).

|
|

|
Definice
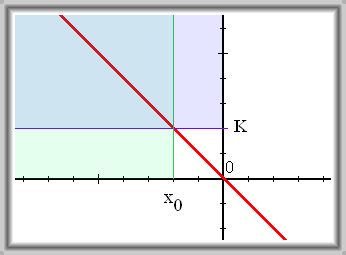
Řekneme, že funkce \(f\) má v nevlastním bodě \(- \infty\) nevlastní limitu \(- \infty\) právě tehdy, když
Značení: \(\lim_{x \to -\infty} f(x) = -\infty\)
Čteme: Limita funkce \(f\) pro \(x\) blížící se k \(- \infty\) je rovna \(- \infty\)
Poznámka
Ke každému reálnému číslu \(K\) existuje takové reálné číslo \(x_0\), že pro všechna reálná \(x \lt x_0\) platí \(f(x) \lt K\).

|
|

|
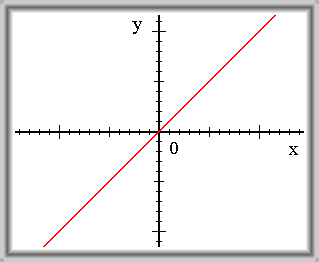
Lepší představu lze získat z následujících grafů funkcí
\(f(x) = x\)
\(\lim_{x \to -\infty} f(x) = -\infty\) \(\lim_{x \to +\infty} f(x) = +\infty\)
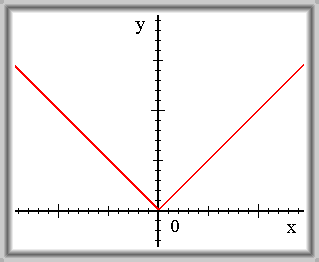
\(f(x) = |x|\)
\(\lim_{x \to -\infty} f(x) = +\infty\) \(\lim_{x \to +\infty} f(x) = +\infty\)
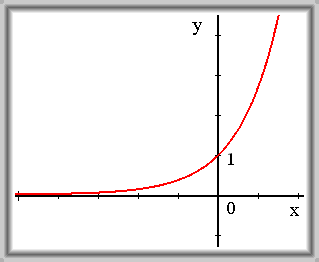
\(f(x) = e^x\)
\(\lim_{x \to +\infty} f(x) = +\infty\)
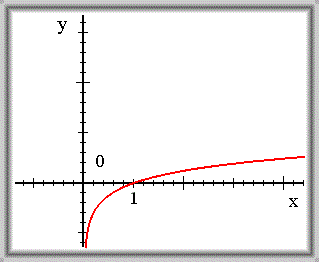
\(f(x) = \mathrm{log} x\)
\(\lim_{x \to +\infty} f(x) = +\infty\)
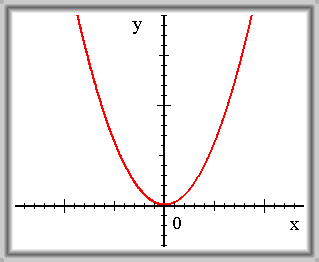
\(f(x) = x^2\)
\(\lim_{x \to -\infty} f(x) = +\infty\) \(\lim_{x \to +\infty} f(x) = +\infty\)
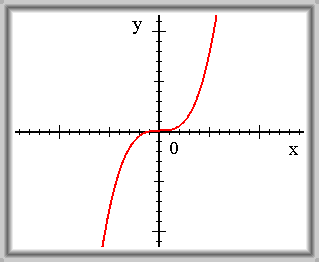
\(f(x) = x^3\)
\(\lim_{x \to -\infty} f(x) = -\infty\) \(\lim_{x \to +\infty} f(x) = +\infty\)