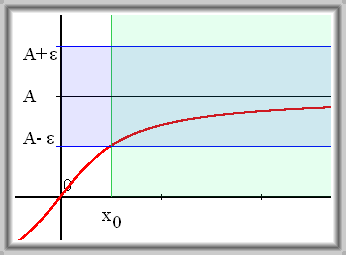
Pro libovolné kladné číslo \(\varepsilon\) existuje reálné číslo \(x_0\) takové, že pro každé reálné číslo \(x \gt x_0\), leží \(f\)(\(x\)) v \(\varepsilon\)-okolí čísla \(A\).
Vlastní limita v nevlastním bodě
Definice
Řekneme, že funkce \(f\) má v bodě \(+\infty\) limitu \(A\) \(\in \mathbb{R}\) právě tehdy, když
Značení: \(\lim_{x \to +\infty} f(x) = A\)
Čteme: Limita funkce \(f\) pro \(x\) blížící se k \(+\infty\) je rovna \(A\)
Poznámka
|
|
|
Obr. 3.13: Vlastní limita funkce v nevlastním bodě \(+ \infty\)
Definice
Řekneme, že funkce \(f\) má v bodě \(-\infty\) limitu \(A\) \(\in \mathbb{R}\) právě tehdy, když
Značení: \(\lim_{x \to -\infty} f(x) = A\)
Čteme: Limita funkce \(f\) pro \(x\) blížící se k \(-\infty\) je rovna \(A\)
Poznámka
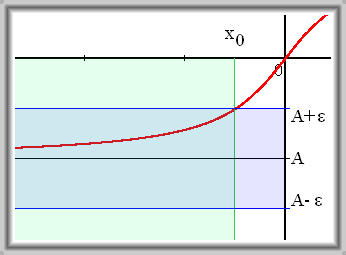
Pro libovolné kladné číslo \(\varepsilon\) existuje reálné číslo \(x_0\) takové, že pro každé reálné číslo \(x \lt x_0\), leží \(f\)(\(x\)) v \(\varepsilon\)-okolí čísla \(A\).
|
|
|
|
|
Obr. 3.14: Vlastní limita funkce v nevlastním bodě \(- \infty\)
Názornou představu lze získat z následujících grafů funkcí
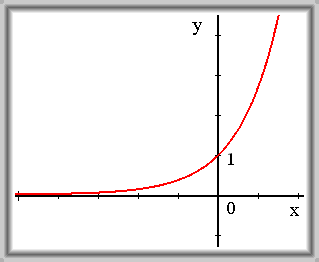
\(f(x) = e^x\)
\(\lim_{x \to -\infty} f(x) = 0\)
Obr. 3.15: \(f(x) = e^x\)
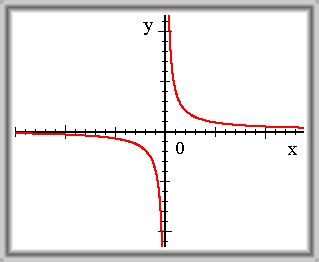
\(f(x) = \frac {1} {x}\)
\(\lim_{x \to -\infty} f(x) = 0\) \(\lim_{x \to +\infty} f(x) = 0\)
Obr. 3.16: \(f(x) = \frac {1} {x}\)
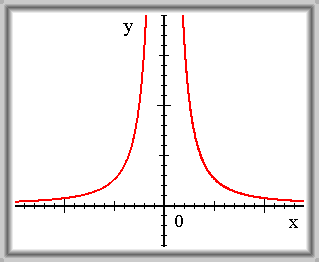
\(f(x) = \frac {1} {x^2}\)
\(\lim_{x \to -\infty} f(x) = 0\) \(\lim_{x \to +\infty} f(x) = 0\)
Obr. 3.17: \(f(x) = \frac {1} {x^2}\)
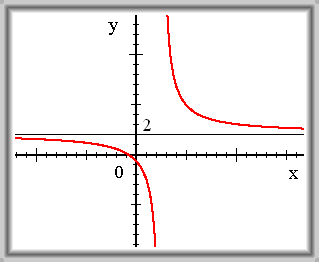
\(f(x) = \frac {2x + 2} {x - 2,5}\)
\(\lim_{x \to -\infty} f(x) = 2\) \(\lim_{x \to +\infty} f(x) = 2\)
Obr. 3.18: \(f(x) = \frac {(2x + 2)} {(x - 2,5)}\)
