Limita a spojitost

Věta

Pokud má funkce v daném bodě limitu, pak je tato limita jednoznačná.

zobraz důkaz schovej důkaz

---

Dokážeme sporem.
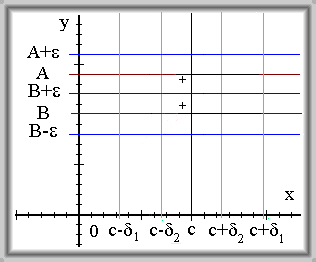
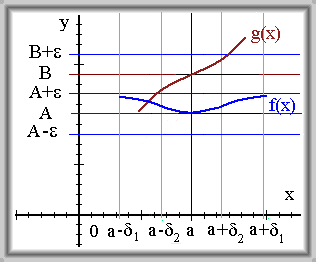
Nechť \(\lim_{x \to c} f(x) = A\) a zároveň \(\lim_{x \to c} f(x) = B\)
Předpokládejme, že \(A \neq B\). Pak mohou nastat dvě možnosti

1. \(A \gt B\)
2. \(A \lt B\)

Ad 1.

\(A,\,B \in \mathbb{R}\):
Zvolme \(\varepsilon, \, \varepsilon = \frac {A - B} {2}\).
\(\exists \delta_{1} \gt 0 \quad \forall x, \, x \in \mathrm{P}(c,\,\delta_{1}) \Rightarrow A - \varepsilon \lt f(x) \lt A + \varepsilon\)
\(\exists \delta_{2} \gt 0 \quad \forall x, \, x \in \mathrm{P}(c,\,\delta_{2}) \Rightarrow B - \varepsilon \lt f(x) \lt B + \varepsilon\)
Definujme \(\delta,\,\delta = \mathrm{min}(\delta_{1},\,\delta_{2})\).
Pro každé \(x \in \mathrm{P}(c,\,\delta)\) tedy platí: \(f(x) < B + \varepsilon = A - \varepsilon \lt f(x)\), což je spor, takže musí být \(A = B\).


Jedna hodnota vlastní, jedna nevlastní, např. \(A = +\infty,\,B \in \mathbb{R}\).
\(\exists \delta_{1} \gt 0 \quad \forall x, \, x \in \mathrm{P}(c,\,\delta_{1}) \Rightarrow |B + 1| \lt f(x)\)
Kdyby bylo \(B + 1 = 0\), pak použijeme \(B + 2\).
\(\exists \delta_{2} \gt 0 \quad \forall x, \, x \in \mathrm{P}(c,\,\delta_{2}) \Rightarrow |B - 1| \lt f(x) \lt B + 1\)
Definujme \(\delta,\,\delta = \mathrm{min}(\delta_{1},\,\delta_{2})\).
Pro každé \(x \in \mathrm{P}(c,\,\delta)\) tedy platí: \(f(x) < B + 1 \leq |B + 1| \lt f(x)\), což je spor.

Obě limity nevlastní, navzájem různé, \(A = +\infty,\,B = -\infty\).
\(\exists \delta_{1} \gt 0 \quad \forall x, \, x \in \mathrm{P}(c,\,\delta_{1}) \Rightarrow 1 \lt f(x)\)
\(\exists \delta_{2} \gt 0 \quad \forall x, \, x \in \mathrm{P}(c,\,\delta_{2}) \Rightarrow f(x) \lt -1\)
Definujme \(\delta,\,\delta = \mathrm{min}(\delta_{1},\,\delta_{2})\).
Pro každé \(x \in \mathrm{P}(c,\,\delta)\) tedy platí: \(f(x) < -1 \lt 1 \lt f(x)\), což je spor.

Obdobně ad 2.

Věta o limitě dvou funkcí

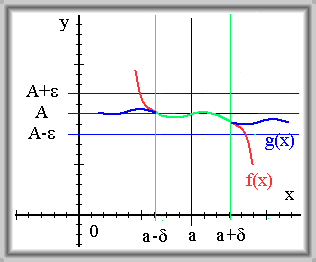
Nechť \(\lim_{x \to a} g(x) = A\) a \(\exists \delta \gt 0\) tak, že \(\forall x \in \mathrm{P}(a,\,\delta)\) platí \(f(x) = g(x)\). Potom \(\lim_{x \to a} f(x) = \lim_{x \to a} g(x) = A.\)

zobraz důkaz schovej důkaz

---

Z definice limity ověříme, že \(\lim_{x \to a} f(x) = A.\)
Nechť je libovoně zvoleno \(\varepsilon \gt 0\).
Pak z předpokladu \(\lim_{x \to a} g(x) = A\) plyne

\(\exists \delta_{1} \gt 0 \quad \forall x \, x \in \mathrm{P}(c,\,\delta_{1}) \Rightarrow g(x) \in \mathrm{U}(A,\,\varepsilon)\)

Zvolme \(\delta_{2},\,\delta_{2} = \mathrm{min}(\delta_{1},\,\delta)\). Tedy \(\mathrm{P}(a,\,\delta_{2})\) je výsledek průniku \(\mathrm{P}(a,\,\delta_{1})\) a \(\mathrm{P}(a,\,\delta)\).
Pro každé \(x \in \mathrm{P}(a,\,\delta)\) platí:
\(f(x) = g(x) \in \mathrm{U}(A,\,\varepsilon)\).
A tedy skutečně \(\lim_{x \to a} f(x) = A\)

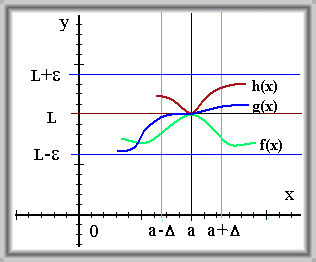
Věta o strážích (někdy také o policistech či o třech limitách)

Nechť \(\exists \delta \gt 0 \quad \forall x \in \mathrm{P}(a,\,\delta)\) platí \(f(x) \leq g(x) \leq h(x)\) a \(\lim_{x \to a} f(x) = \lim_{x \to a} h(x) = L.\)
Pak \(\exists \lim_{x \to a} g(x)\) a platí \(\lim_{x \to a} g(x) = L.\)

zobraz důkaz schovej důkaz

---

Z definice limity ověříme, že \(\lim_{x \to a} g(x) = L.\)

A. Pro \(L \in \mathbb{R}\).
Nechť \(\varepsilon \gt 0\) je zvoleno libovolně pevně.
Pak
\(\exists \delta_{1} \gt 0 \quad \forall x \, x \in \mathrm{P}(a,\,\delta_{1}) \Rightarrow L - \varepsilon \lt f(x) \lt L + \varepsilon\)
\(\exists \delta_{2} \gt 0 \quad \forall x \, x \in \mathrm{P}(a,\,\delta_{2}) \Rightarrow L - \varepsilon \lt h(x) \lt L + \varepsilon\)

Z předpokladů věty víme, že
\(\exists \delta \gt 0 \quad \forall x \in \mathrm{P}(a,\,\delta) \quad f(x) \leq g(x) \leq h(x)\).

Zvolme \(\Delta,\,\Delta = \mathrm{min}(\delta_1,\,\delta_2,\,\delta)\).

Pak pro \(x \in \mathrm{P}(a,\,\Delta)\) platí:
\(L - \varepsilon \lt f(x) \leq g(x) \leq h(x) \lt L + \varepsilon\)
\(L - \varepsilon \lt g(x) \lt L + \varepsilon\)
a tedy \(g(x) \in \mathrm{U}(L,\,\varepsilon)\), což znamená, že \(\lim_{x \to a} g(x) = L\)





B. Pro \(L = +\infty\).
Nechť \(K\) je zvoleno libovolně pevně.
Pak
\(\exists \delta_{1} \gt 0 \quad \forall x \, x \in \mathrm{P}(a,\,\delta_{1}) \Rightarrow K \lt f(x)\)

Z předpokladů věty víme, že
\(\exists \delta \gt 0 \quad \forall x \in \mathrm{P}(a,\,\delta) \quad f(x) \leq g(x) \leq h(x)\).

Zvolme \(\Delta,\,\Delta = \mathrm{min}(\delta_1,\,\delta)\).

Pak pro \(x \in \mathrm{P}(a,\,\Delta)\) platí:
\(K \lt f(x) \leq g(x) \leq h(x)\)
\(K \lt g(x)\)
a tedy \(\lim_{x \to a} g(x) = L\)

Věta

Nechť \(\lim_{x \to a} f(x) = A \lt B = \lim_{x \to a} g(x).\)
Pak \(\exists \delta \gt 0 \quad \forall x \in \mathrm{P}(a,\,\delta)\) platí \(f(x) \lt g(x)\).

zobraz důkaz schovej důkaz

---

1. \(A,\,B \in \mathbb{R}\).

Zvolme \(\varepsilon,\,\varepsilon = \frac{B - A}{2}\).
Pak
\(\exists \delta_{1} \gt 0 \quad \forall x \, x \in \mathrm{P}(a,\,\delta_{1}) \Rightarrow A - \varepsilon \lt f(x) \lt A + \varepsilon\)
\(\exists \delta_{2} \gt 0 \quad \forall x \, x \in \mathrm{P}(a,\,\delta_{2}) \Rightarrow B - \varepsilon \lt g(x) \lt B + \varepsilon\)

Definujme \(\delta,\,\delta = \mathrm{min}(\delta_1,\,\delta_2)\).

Pro každé \(x \in \mathrm{P}(a,\,\delta)\) platí:
\(f(x) \lt A + \varepsilon = B - \varepsilon \lt g(x)\)
\(f(x) \lt g(x)\)




2. \(A \in \mathbb{R},\,B = +\infty\).

\(\exists \delta_{1} \gt 0 \quad \forall x \, x \in \mathrm{P}(a,\,\delta_{1}) \Rightarrow A - 1 \lt f(x) \lt A + 1\)
Kdyby bylo \(A + 1 = 0\), pak použijeme \(A + 2\).
\(\exists \delta_{2} \gt 0 \quad \forall x \, x \in \mathrm{P}(a,\,\delta_{2}) \Rightarrow |A + 1| \lt g(x)\)

Definujme \(\delta,\,\delta = \mathrm{min}(\delta_1,\,\delta_2)\).

Pro každé \(x \in \mathrm{P}(a,\,\delta)\) tedy platí:
\(f(x) \lt A + 1 \leq |A + 1| \lt g(x)\)


3. \(A = -\infty,\,B = +\infty\).

\(\exists \delta_{1} \gt 0 \quad \forall x \, x \in \mathrm{P}(a,\,\delta_{1}) \Rightarrow f(x) \lt -1\)
\(\exists \delta_{2} \gt 0 \quad \forall x \, x \in \mathrm{P}(a,\,\delta_{2}) \Rightarrow 1 \lt g(x)\)

Definujme \(\delta,\,\delta = \mathrm{min}(\delta_1,\,\delta_2)\).

Pro každé \(x \in \mathrm{P}(a,\,\delta)\) tedy platí:
\(f(x) \lt -1 \lt 1 \lt g(x)\)

Věta

Nechť existuje \(\delta \gt 0\) tak, že \(\forall x \in \mathrm{P}(a,\,\delta)\) platí \(f(x) \leq g(x)\) a nechť \(\lim_{x \to a} f(x) = A\) a
\(\lim_{x \to a} g(x) = B.\)
Potom platí \(A \leq B\).

Věta

Nechť \(\lim_{x \to a} f(x) = A\) a \(A \in \mathbb{R}\).
Potom \(\exists \delta \gt 0\) tak, že funkce \(f\) je omezená na \(\mathrm{P}(a,\,\delta)\).

zobraz důkaz schovej důkaz

---

Zvolme \(\varepsilon = 1\)
Pak \(\exists \delta \gt 0\) tak, že pro každé \(x \in \mathrm{P}(a,\,\delta)\) platí:
\(A - 1 \lt f(x) \lt A + 1\)
A tedy funkce \(f\) je na prstencovém okolí bodu \(a\) omezená.

Věta

Nechť \(\lim_{x \to a} f(x) = 0\) a \(\exists \delta \gt 0\) tak, že funkce \(g(x)\) je omezená na \(\mathrm{P}(a,\,\delta)\). Pak \(\lim_{x \to a} f(x) \cdot g(x) = 0.\)

zobraz důkaz schovej důkaz

---

Z předpokladů věty plyne
\(\exists K \gt 0\) tak, že pro každé \(x \in \mathrm{P}(a,\,\delta)\) platí: \(|g(x)| \lt K\)

Zvolme libovolně pevně \(\varepsilon \gt 0\) a definujme \(\varepsilon_{1},\,\varepsilon_{1} = \frac{\varepsilon}{K}\)
Z definice limity dostaneme
\(\exists \delta_1 \gt 0 \quad \forall x \quad x \in \mathrm{P}(a,\,\delta_1) \Rightarrow -\varepsilon_1 \lt f(x) \lt \varepsilon_1\)
Zvolme \(\Delta,\,\Delta = \mathrm{min}(\delta_1,\,\delta)\).

Pro každé \(x \in \mathrm{P}(a,\,\Delta)\) tedy platí:
\(|f(x) \cdot g(x) - 0| = |f(x)||g(x)| \lt \varepsilon_1K = \frac{\varepsilon}{K}K = \varepsilon\)
a tedy \(\lim_{x \to a} f(x) \cdot g(x) = 0.\)

Věta

Nechť \(\lim_{x \to a} f(x) = A.\) Potom \(\lim_{x \to a} |f(x)| = |A|\).

Věta

Nechť \(\lim_{x \to a} f(x) = A\) a \(\lim_{x \to a} g(x) = B.\) Potom

1. \(\lim_{x \to a} (f(x) \pm g(x)) = A \pm B\)
2. \(\lim_{x \to a} f(x)g(x) = AB\)
3. Je-li \(B \neq 0 \quad \lim_{x \to a} \frac {f(x)}{g(x)} = \frac {A}{B}\)

Věta

Nechť \(\lim_{x \to a} f(x) = 0\) a \(\exists \delta \gt 0 \quad x \in \mathrm{P}(a,\,\delta) \Rightarrow f(x) \gt 0\), pak \(\lim_{x \to a} \frac {1}{f(x)} = + \infty.\)

Věta

Je-li \(\lim_{x \to a} g(x) = A\) a funkce \(f\) je spojitá v bodě \(A\), potom \(\lim_{x \to a} f(g(x)) = f(A).\)

Věta

Nechť \(\lim_{x \to a} g(x) = A\) a \(\lim_{y \to A} f(y) = B\) a \(\exists \delta \gt 0 \quad x \in \mathrm{P}(a,\,\delta) \Rightarrow g(x) \neq A\). Potom \(\lim_{x \to a} f(g(x)) = B.\)