Lokální extrémy pomocí 2. derivace
V této podkapitole se naučíte nalézat lokální extrémy různých funkcí pomocí 2. derivace. Tato metoda je někdy rychlejší, než hledání lokálních extrémů tabulkovou metodou. Existují však případy, kdy se touto metodou nedá ověřit, zda je nějaký bod lokálním extrémem, i když tabulkovou metodou to možné ověřit je. S takovým případem se setkáte v Příkladě 2. Opět zde platí předpoklady uvedené v podkapitole Předpoklady. Než se pustíte do příkladů a úloh, zkuste se nejdříve procvičit, pokud jste to již neudělali, v podkapitole Druhá derivace, příklad a úlohy.
Nejprve je uvedena teorie a pak příklady a úlohy.
Teoretická část
Věta
Má-li funkce \(f\) ve vnitřním bodě \(x_0\) zkoumaného intervalu lokální extrém a existuje-li v tomto bodě derivace \(f^{\prime}(x_0)\), pak platí, že \(f^{\prime}(x_0) = 0\), tj., že \(x_0\) je stacionární bod.
Poznámka k předchozí větě
Opačné tvrzení neplatí. V podkapitole Lokální extrémy tabulkovou metodou jsme se setkali v Příkladě 4 a Úloze 4 s funkcemi, které měly ve vnitřních bodech zkoumaného intervalu spojitosti stacionární bod, ale neměly v něm lokální extrém.
Následující věta je základním teoretickým východiskem pro hledání lokálních extrémů pomocí 2. derivace.
Věta
Nechť \(x_0\) je stacionárním bodem funkce \(f\) a nechť existuje v bodě \(x_0\) její druhá derivace \(f^{\prime\prime}\).
Je-li \(f^{\prime\prime}(x_0) \lt 0\), pak má funkce \(f\) v bodě \(x_0\) ostré lokální maximum.
Je-li \(f^{\prime\prime}(x_0) \gt 0\), pak má funkce \(f\) v bodě \(x_0\) ostré lokální minimum.
Poznámka k předchozí větě
Je-li \(f^{\prime\prime}(x_0) = 0\), nelze na základě toho o existenci lokálního extrému rozhodnout. Řešením pak může být použití tabulkové metody.

Příklady a úlohy
Značení
V následujících příkladech a úlohách budeme používat tato značení:
| LMax | ..... | množina obsahující dvojice [xmax,ymax], kde xmax je bod, ve kterém nabývá zkoumaná funkce ostré lokální maximum, a ymax je hodnota tohoto maxima; |
| LMin | ..... | množina obsahující dvojice [xmin,ymin], kde xmin je bod, ve kterém nabývá zkoumaná funkce ostré lokální minimum, a ymin je hodnota tohoto minima. |
Příklad 1
Najděte ostré lokální extrémy funkce \(f: y = 2x^3-3x^2-36x + 5\) pomocí druhé derivace.
Řešení
Definiční obor: \((-\infty,\infty)\).
První derivace: \(f^{\prime}(x) = 6x^2-6x-36 = 6(x^2-x+6) = 6(x-3)(x+2)\).
Stacionární body: \(-2; 3\).
Druhá derivace: \(f^{\prime\prime}(x) = 12x-6\).
Zjišťování ostrých lokálních extrémů pomocí druhé derivace:
* výpočty hodnot druhé derivace ve stacionárních bodech;
* zjištění, zda lze extrémy určit pomocí druhé derivace, a v případě, že ano, jakého jsou typu;
* určení funkční hodnoty v bodech, v nichž se nacházejí extrémy.
| \(-2\) | \(3\) |
|---|---|
| \(f^{\prime\prime}(-2) = -30 \lt 0\) ostré lok. maximum \(f(-2) = 49\) |
\(f^{\prime\prime}(3) = 30 \gt 0\) ostré lok. minimum \(f(3) = -76\) |
Závěr: LMax = { [-2,49] }, LMin = { [3,-76] }.
Úloha 1
Najděte ostré lokální extrémy funkce \(f: y = x^2+6x\) pomocí druhé derivace.
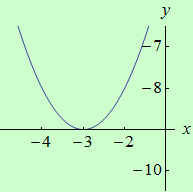 graf funkce |
Definiční obor:
První derivace:
Stacionární body:
Druhá derivace:
Zjišťování ostrých lokálních extrémů pomocí druhé derivace:
Závěr:
Úloha 2
Najděte ostré lokální extrémy funkce \(f: y = 2x^3+3x^2-3\) pomocí druhé derivace.
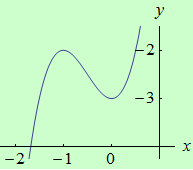 graf funkce |
Definiční obor:
První derivace:
Stacionární body:
Druhá derivace:
Zjišťování ostrých lokálních extrémů pomocí druhé derivace:
Závěr:
Příklad 2
Najděte ostré lokální extrémy funkce \(f: y = x^5-5x^4\) pomocí druhé derivace.
Řešení
Definiční obor: \((-\infty,\infty)\).
První derivace: \(f^{\prime}(x) = 5x^4-20x^3 = 5x^3(x-4)\).
Stacionární body: \(0; 4\).
Druhá derivace: \(f^{\prime\prime}(x) = 20x^3-60x^2\).
Zjišťování ostrých lokálních extrémů pomocí druhé derivace:
* výpočty hodnot druhé derivace ve stacionárních bodech;
* zjištění, zda lze extrémy určit pomocí druhé derivace, a v případě, že ano, jakého jsou typu;
* určení funkční hodnoty v bodech, v nichž se nacházejí extrémy.
| \(0\) | \(4\) |
|---|---|
| \(f^{\prime\prime}(0) = 0\) pomocí 2. derivace se nedá rozhodnout |
\(f^{\prime\prime}(4) = 320 \gt 0\) ostré lok. minimum \(f(4) = -256\) |
Závěr: LMin = { [4,-256] }.
Poznámka: Funkce má v bodě \(x = 0\) ostré lokální maximum.
Úloha 3
Najděte ostré lokální extrémy funkce \(f: y = -3x^4-4x^3\) pomocí druhé derivace.
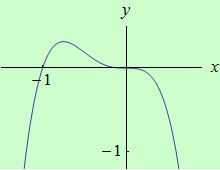 graf funkce |
Definiční obor:
První derivace:
Stacionární body:
Druhá derivace:
Zjišťování ostrých lokálních extrémů pomocí druhé derivace:
Závěr:
Poznámka:
Příklad 3
Najděte ostré lokální extrémy funkce \(f: y = 2x-\sin{2x}\) pomocí druhé derivace na intervalu \((-{\large\frac{\pi}{2}},{\large\frac{\pi}{2}})\).
Řešení
Definiční obor: \((-{\large\frac{\pi}{2}},{\large\frac{\pi}{2}})\).
První derivace: \(f^{\prime}(x) = 2-2\cos{2x} = 2(1-\cos{2x})\).
Stacionární body: \(0\).
Druhá derivace: \(f^{\prime\prime}(x) = 4\sin{2x}\).
Zjišťování ostrých lokálních extrémů pomocí druhé derivace:
* výpočty hodnot druhé derivace ve stacionárních bodech;
* zjištění, zda lze extrémy určit pomocí druhé derivace, a v případě, že ano, jakého jsou typu;
* určení funkční hodnoty v bodech, v nichž se nacházejí extrémy.
| \(0\) |
|---|
| \(f^{\prime\prime}(0) = 0\) pomocí 2. derivace se nedá rozhodnout |
Závěr: Pomocí 2. derivace se nepodařilo najít žádné ostré lokální extrémy.
Poznámka: Funkce nemá v bodě \(x = 0\) ani lokální maximum ani lokální minimum.
Úloha 4
Najděte ostré lokální extrémy funkce \(f: y = 2x+\cos{2x}\) pomocí druhé derivace na intervalu \((0,\pi)\).
Definiční obor:
První derivace:
Stacionární body:
Druhá derivace:
Zjišťování ostrých lokálních extrémů pomocí druhé derivace:
Závěr:
Poznámka:
Příklad 4
Najděte ostré lokální extrémy funkce \(f: y = e^x(x^2-2x+1)\) pomocí druhé derivace.
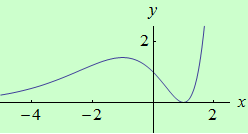 graf funkce |
Definiční obor: \((-\infty,\infty)\).
První derivace: \(f^{\prime}(x) = e^x(x^2-1)\).
Stacionární body: \(-1; 1\).
Druhá derivace: \(f^{\prime\prime}(x) = e^x(x^2+2x-1)\).
Zjišťování ostrých lokálních extrémů pomocí druhé derivace:
* výpočty hodnot druhé derivace ve stacionárních bodech;
* zjištění, zda lze extrémy určit pomocí druhé derivace, a v případě, že ano, jakého jsou typu;
* určení funkční hodnoty v bodech, v nichž se nacházejí extrémy.
| \(-1\) | \(1\) |
|---|---|
| \(f^{\prime\prime}(-1) = -2e^{-1} \lt 0\) ostré lok. maximum \(f(-1) = 4e^{-1}\) |
\(f^{\prime\prime}(1) = 2e \gt 0\) ostré lok. minimum \(f(1) = 0\) |
Závěr: LMax = { \([-1,4e^{-1}]\) }, LMin = { \([1,0]\) }.
Úloha 5
Najděte ostré lokální extrémy funkce \(f: y = e^x(x^2+1)\) pomocí druhé derivace.
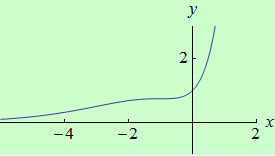 graf funkce |
Definiční obor:
První derivace:
Stacionární body:
Druhá derivace:
Zjišťování ostrých lokálních extrémů pomocí druhé derivace:
Závěr:
Poznámka:
Příklad 5
Najděte ostré lokální extrémy funkce \(f: y = \large\frac{\ln{x}}{x}\) pomocí druhé derivace.
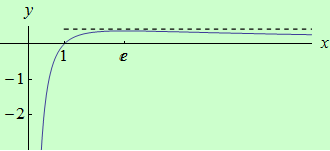 graf funkce |
Definiční obor: \((0,\infty)\).
První derivace: \(f^{\prime}(x) = \large\frac{1-\ln{x}}{x^2}\).
Stacionární body: \(e\).
Druhá derivace: \(f^{\prime\prime}(x) = \large\frac{-3+2\ln{x}}{x^3}\).
Zjišťování ostrých lokálních extrémů pomocí druhé derivace:
* výpočty hodnot druhé derivace ve stacionárních bodech;
* zjištění, zda lze extrémy určit pomocí druhé derivace, a v případě, že ano, jakého jsou typu;
* určení funkční hodnoty v bodech, v nichž se nacházejí extrémy.
| \(e\) |
|---|
| \(f^{\prime\prime}(e) = -{\large\frac{1}{e^3}} \lt 0\) ostré lok. maximum \(f(e) = \large\frac{1}{e}\) |
Závěr: LMax = { \([e,e^{-1}]\) }.
Úloha 6
Najděte ostré lokální extrémy funkce \(f: y = \ln^2{x}\) pomocí druhé derivace.
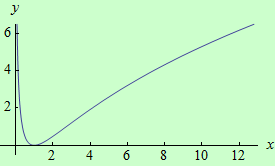 graf funkce |
Definiční obor:
První derivace:
Stacionární body:
Druhá derivace:
Zjišťování ostrých lokálních extrémů pomocí druhé derivace:
Závěr:
Úloha 7
Najděte ostré lokální extrémy funkce \(f: y = 8\ln{x}-x^2\) pomocí druhé derivace.
Definiční obor:
První derivace:
Stacionární body:
Druhá derivace:
Zjišťování ostrých lokálních extrémů pomocí druhé derivace:
Závěr:
Příklad 6
Najděte ostré lokální extrémy funkce \(f: y = 4\sqrt{x}-x\) pomocí druhé derivace.
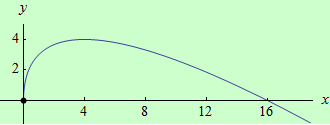 graf funkce |
Definiční obor: \( \langle 0,\infty)\).
První derivace: \(f^{\prime}(x) = {\large\frac{2}{\sqrt{x}}} - 1\).
Stacionární body: \(4\).
Druhá derivace: \(f^{\prime\prime}(x) = -{\large\frac{1}{\sqrt{x^3}}}\).
Zjišťování ostrých lokálních extrémů pomocí druhé derivace:
* výpočty hodnot druhé derivace ve stacionárních bodech;
* zjištění, zda lze extrémy určit pomocí druhé derivace, a v případě, že ano, jakého jsou typu;
* určení funkční hodnoty v bodech, v nichž se nacházejí extrémy.
| \(4\) |
|---|
| \(f^{\prime\prime}(4) = -{\large\frac{1}{8}} \lt 0\) ostré lok. maximum \(f(4) = 4\) |
Závěr: LMax = { [4,4] }.
Poznámka: Funkce má ostré lokální minimum v bodě \(x = 0\). Ten však není stacionární.
Úloha 8
Najděte ostré lokální extrémy funkce \(f: y = 8\sqrt{x}-x\) pomocí druhé derivace.
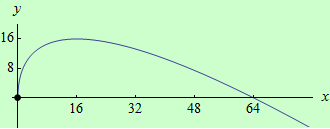 graf funkce |
Definiční obor:
První derivace:
Stacionární body:
Druhá derivace:
Zjišťování ostrých lokálních extrémů pomocí druhé derivace:
Závěr:
Poznámka:
Úloha 9
Najděte ostré lokální extrémy funkce \(f: y = 3x^4-4x^3-12x^2\) pomocí druhé derivace.
Definiční obor:
První derivace:
Stacionární body:
Druhá derivace:
Zjišťování ostrých lokálních extrémů pomocí druhé derivace:
Závěr:
