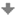Globální extrémy
Tato část navazuje na podkapitolu Lokální extrémy tabulkovou metodou. Naučíte se zde nalézat globální extrémy různých funkcí. Předpokladem pro pochopení této látky je zvládnutí příkladů a úloh z podkapitoly Lokální extrémy tabulkovou metodou. Budeme hledat globální extrémy vždy jen na jednom intervalu spojitosti. Opět platí předpoklady uvedené v podkapitole Předpoklady.
Nejprve je uvedena teorie a pak příklady a úlohy.
Teoretická část
Definice
Funkce \(f\) má na intervalu \(I\) v bodě \(x_0\) globální maximum, jestliže pro všechna \(x \in I\) platí: \(f(x) \leq f(x_0)\).
Funkce \(f\) má na intervalu \(I\) v bodě \(x_0\) globální minimum, jestliže pro všechna \(x \in I\) platí: \(f(x) \geq f(x_0)\).
Globální maxima a minima nazýváme souhrnně globální extrémy.
Věta
Je-li funkce \(f\) spojitá na uzavřeném intervalu, pak tam má globální maximum i minimum.
Poznámky k předchozí větě
Je-li funkce spojitá na otevřeném intervalu, nemusí tam mít žádné extrémy.
Ilustrace: Na intervalu \((0,1)\) nemá funkce \(f: y = x\) žádný lokální ani globální extrém.
Je-li funkce spojitá na polouzavřeném intervalu, pak za Předpokladu 3 z podkapitoly Předpoklady platí, že tam má vždy alespoň jeden globální extrém. Z důvodu složitosti však nebudeme toto tvrzení dokazovat.
Pokud bychom o funkci spojité na polouzavřeném intervalu nic nepředpokládali, pak na takovém intervalu nemusí mít žádné globální extrémy.
| Ilustrace: | Na intervalu \(\langle 0,1 )\) nemá funkce \(f: y = x \sin\dfrac{1}{1-x}\) žádný globální extrém. |
| Funkce podobného typu je zobrazena na následujícím obrázku: |
Věta
Je-li funkce \(f\) spojitá na uzavřeném intervalu, pak jejím globálním maximem je maximum ze všech lokálních maxim a jejím globálním minimem je minimum ze všech lokálních minim.
Věta
Jestliže u funkce spojité na otevřeném nebo polouzavřeném intervalu neexistuje lokální maximum, pak tam neexistuje ani globální maximum. Podobně neexistence lokálního minima znamená neexistenci globálního minima.
Poznámka k předchozí větě
Předchozí věta vyplývá ze skutečnosti, že každý globální extrém je i lokálním extrémem.
Připomínám, že o zkoumaných funkcích předpokládáme, že na zkoumaném intervalu spojitosti je nulový nebo malý konečný počet stacionárních bodů a bodů, v nichž není derivace definována.
Za výše uvedeného předpokladu platí následující tři věty:
Věta
Každý lokální extrém je ostrým lokálním extrémem.
Věta
Je-li funkce \(f\) spojitá na polouzavřeném intervalu \((a,b\rangle\), pak existuje \(\large\lim\limits_{x \to a+}\normalsize f(x)\).
Je-li funkce \(f\) spojitá na polouzavřeném intervalu \(\langle a,b)\), pak existuje \(\large\lim\limits_{x \to b-}\normalsize f(x)\).
Je-li funkce \(f\) spojitá na otevřeném intervalu \((a,b)\), pak existují obě předchozí limity.
Věta
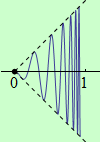
a) Nechť funkce \(f\) je spojitá na polouzavřeném intervalu \((a,b\rangle\) a má alespoň jedno lokální maximum. Na daném intervalu neexistuje globální maximum, jestliže je maximum ze všech lokálních maxim nižší, než \(\large\lim\limits_{x \to a+}\normalsize f(x)\), viz následující obrázek:
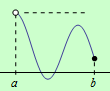
b) Nechť funkce \(f\) je spojitá na polouzavřeném intervalu \((a,b\rangle\) a má alespoň jedno lokální minimum. Na daném intervalu neexistuje globální minimum, jestliže je minimum ze všech lokálních minim vyšší, než \(\large\lim\limits_{x \to a+}\normalsize f(x)\), viz následující obrázek:
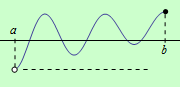
c) Obdobná tvrzení platí, je-li funkce \(f\) spojitá na polouzavřeném intervalu \(\langle a,b)\).
d) Nechť funkce \(f\) je spojitá na otevřeném intervalu \((a,b)\) a má alespoň jedno lokální maximum. Na daném intervalu neexistuje globální maximum, jestliže je maximum ze všech lokálních maxim nižší, než \(\large\lim\limits_{x \to a+}\normalsize f(x)\) nebo \(\large\lim\limits_{x \to b-}\normalsize f(x)\), viz následující obrázek:
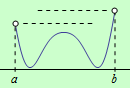
e) Nechť funkce \(f\) je spojitá na otevřeném intervalu \((a,b)\) a má alespoň jedno lokální minimum. Na daném intervalu neexistuje globální minimum, jestliže je minimum ze všech lokálních minim vyšší, než \(\large\lim\limits_{x \to a+}\normalsize f(x)\) nebo \(\large\lim\limits_{x \to b-}\normalsize f(x)\), viz následující obrázek:
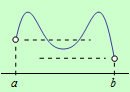
Příklady a úlohy
Pro hledání globálních extrémů na daném intervalu spojitosti je třeba nalézt na tomto intervalu všechny lokální extrémy. K tomuto účelu je nejvhodnější použít tabulkovou metodu. Kromě toho je nutné vypočítat limity zkoumané funkce v krajních bodech intervalu, pokud tyto body do tohoto intervalu nepatří.
V Příkladu 1 a Úloze 1 s obrázky však nebudete muset dělat žádné výpočty.
Značení
V následujících příkladech a úlohách budeme používat tato značení:
| GMax | ..... | množina obsahující dvojice [xmax;ymax], kde xmax je bod, ve kterém nabývá zkoumaná funkce globální maximum, a ymax je hodnota tohoto maxima; |
| GMin | ..... | množina obsahující dvojice [xmin;ymin], kde xmin je bod, ve kterém nabývá zkoumaná funkce globální minimum, a ymin je hodnota tohoto minima; |
| L(x/+) | ..... | limita zadané funkce v bodě x zprava; |
| L(x/–) | ..... | limita zadané funkce v bodě x zleva; |
| LKB | ..... | množina obsahující hodnoty příslušných jednostranných limit v těch krajních bodech daného intervalu spojitosti, které do tohoto intervalu nepatři; týká se to otevřených a polouzavřených intervalů spojitosti; (jako „limity v krajních bodech“); |
| LMax | ..... | množina obsahující dvojice [xmax;ymax], kde xmax je bod, ve kterém nabývá zkoumaná funkce ostré lokální maximum, a ymax je hodnota tohoto maxima; |
| LMin | ..... | množina obsahující dvojice [xmin;ymin], kde xmin je bod, ve kterém nabývá zkoumaná funkce ostré lokální minimum, a ymin je hodnota tohoto minima; |
| M | ..... | bod, v němž zkoumaná funkce nabývá ostré lokální maximum; v tabulce v místě pod touto značkou budeme psát hodnotu tohoto maxima; |
| m | ..... | bod, v němž zkoumaná funkce nabývá ostré lokální minimum; v tabulce v místě pod touto značkou budeme psát hodnotu tohoto minima. |
Příklad 1
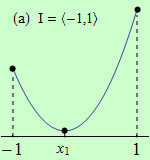
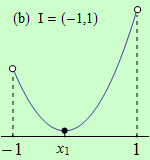
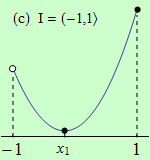
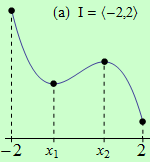
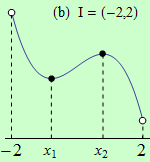
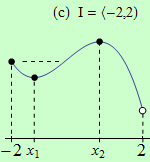
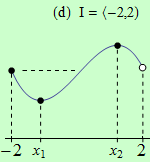
Pro funkce, jejichž grafy jsou zobrazeny v následujících obrázcích, najděte body, v nichž mají na daném intervalu I svá globální maxima a minima.
 |  |  |
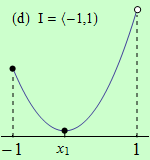 | 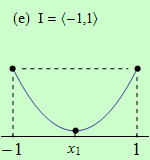 | 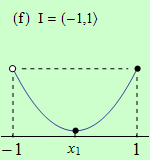 |
Všechny funkce mají na daných intervalech globální minimum v bodě \(x_1\).
Funkce
(a) má globální maximum v bodě \(x = 1\);
(b) nemá globální maximum;
(c) má globální maximum v bodě \(x = 1\);
(d) nemá globální maximum;
(e) má dvě globální maxima v bodech \(x = -1\) a \(x = 1\);
(f) má globální maximum v bodě \(x = 1\).
Úloha 1
Pro funkce, jejichž grafy jsou zobrazeny v následujících obrázcích, najděte body, v nichž mají na daném intervalu I svá globální maxima a minima.
 |  |  |
 | 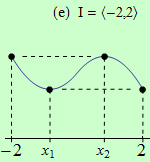 | 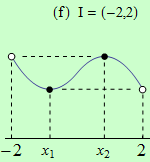 |
Zakrytá řešení odkryjete kliknutím na ně.
(a)
(b)
(c)
(d)
(e)
(f)
Příklad 2
Najděte globální extrémy funkce \(f: y = \cos{x}+\sin{x}\) na intervalu \( \langle 0,2\pi \rangle \).
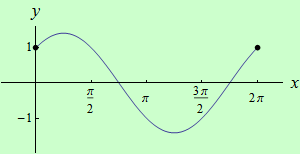 graf funkce |
K nalezení lokálních extrémů použijeme tabulkovou metodu:
Intervaly spojitosti: \( \langle 0,2\pi \rangle \).
Derivace: \(f^{\prime}(x) = -\sin{x} + \cos{x}\).
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti (řešení rovnice \(\sin{x} = \cos{x} \Rightarrow {\rm tg}\:x = 1\)): \(\dfrac{\pi}{4}, \dfrac{5\pi}{4}\).
Tabulka:
| \(0\) | \((0,\dfrac{\pi}{4})\) | \(\dfrac{\pi}{4}\) | \((\dfrac{\pi}{4},\dfrac{5\pi}{4})\) | \(\dfrac{5\pi}{4}\) | \((\dfrac{5\pi}{4},2\pi)\) | \(2\pi\) |
|---|---|---|---|---|---|---|
| m 1 |
\(f^{\prime}(0) = 1 \gt 0\) rostoucí |
M \(\sqrt{2}\) |
\(f^{\prime}(\pi) = -1 \lt 0\) klesající |
m \(-\sqrt{2}\) |
\(f^{\prime}(2\pi) = 1 \gt 0\) rostoucí |
M 1 |
Lokální extrémy: LMax = { \([\dfrac{\pi}{4};\sqrt{2}]\), \([2\pi;1]\) }, LMin = { \([0;1]\), \([\dfrac{5\pi}{4};-\sqrt{2}]\) }.
Globálním maximem funkce \(f\) na uzavřeném intervalu je maximum ze všech lokálních maxim a globálním minimem minimum ze všech lokálních minim.
Závěr: GMax = { \([\dfrac{\pi}{4};\sqrt{2}]\) }, GMin = { \([\dfrac{5\pi}{4};-\sqrt{2}]\) }.
Poznámka
Monotónnost funkce \(f\) na intervalech \((0,\dfrac{\pi}{4})\) a \((\dfrac{5\pi}{4},2\pi)\) jsme testovali pomocí hodnoty derivací v krajních bodech, které do těchto intervalů nepatřily. Tento postup je povolený za předpokladu, že je derivace v krajním bodě definovaná a nenulová.
Úloha 2
Najděte globální extrémy funkce \(f: y = -x^3+6x^2+10\) na intervalu \( \langle {-1},7 \rangle \).
K nalezení lokálních extrémů použijeme tabulkovou metodu:
Intervaly spojitosti:
Derivace:
Body z intervalů spojitosti, v nichž není derivace definována:
Stacionární body z intervalů spojitosti
Tabulka:
Lokální extrémy:
Závěr:
Příklad 3
Najděte globální extrémy funkce \(f: y = \sqrt{x}+\dfrac{4}{x}-2\) na intervalu \((0,7 \rangle \).
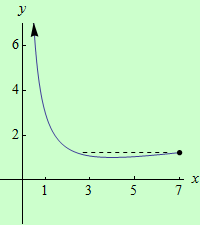 graf funkce |
K nalezení lokálních extrémů použijeme tabulkovou metodu:
Intervaly spojitosti: \((0,7 \rangle \).
Derivace: \(f^{\prime}(x) =\dfrac{1}{2 \sqrt{x}}-\dfrac{4}{x^2}\).
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti (řešení rovnice \(\dfrac{1}{2 \sqrt{x}}=\dfrac{4}{x^2} \Rightarrow (\sqrt{x})^3 = 8\)): 4.
Tabulka:
| \(L(0/+)\) | \((0,4)\) | \(4\) | \((4,7)\) | \(7\) |
|---|---|---|---|---|
| \(+\infty\) |
\(f^{\prime}(1) = -3.5 \lt 0\) klesající |
m \(1\) |
\(f^{\prime}(5) \gt 0\) rostoucí |
M \(\sqrt{7}-\dfrac{10}{7}\) |
Nerovnost \(f^{\prime}(5) = \dfrac{1}{2 \sqrt{5}}-\dfrac{4}{25} \gt 0\) se řeší následovně:
\(\dfrac{1}{2 \sqrt{5}} \gt \dfrac{4}{5^2} \;\;\; \Leftrightarrow \;\;\; \dfrac{1}{4\cdot 5} \gt \dfrac{16}{5^4} \;\;\; \Leftrightarrow \;\;\; 5^3 \gt 4\cdot 16 \;\;\; \Leftrightarrow \;\;\; 125 \gt 64\)
Lokální extrémy: LMax = { \([7;\sqrt{7}-\dfrac{10}{7}]\) }, LMin = { \([4;1]\) }.
Musíme zohlednit limitu funkce \(f\) v bodě \(x = 0\) zprava: LKB = { \(+\infty\) }.
Závěr: GMin = { \([4;1]\) }, globální maximum neexistuje.
Poznámka
Jestliže je příslušná jednostranná limita v krajním bodě intervalu rovna \(+\infty\), pak nemůže existovat globální maximum. Důvodem je, že žádné lokální ani globální maximum nemůže mít hodnotu plus nekonečno.
Podobně, kdyby byla příslušná jednostranná limita v krajním bodě intervalu rovna \(-\infty\), pak nemůže existovat globální minimum.
Úloha 3
Najděte globální extrémy funkce \(f: y = x+\dfrac{4}{x}+5\) na intervalu \( \langle {-5},0)\).
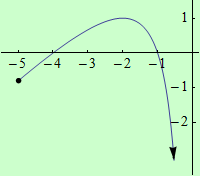 graf funkce |
K nalezení lokálních extrémů použijeme tabulkovou metodu:
Intervaly spojitosti:
Derivace:
Body z intervalů spojitosti, v nichž není derivace definována:
Stacionární body z intervalů spojitosti
Tabulka:
Lokální extrémy:
Závěr:
Úloha 4
Najděte globální extrémy funkce \(f: y = -x^3+3x+1\) na intervalu \((-3,5)\).
K nalezení lokálních extrémů použijeme tabulkovou metodu:
Intervaly spojitosti:
Derivace:
Body z intervalů spojitosti, v nichž není derivace definována:
Stacionární body z intervalů spojitosti
Tabulka:
Lokální extrémy:
Závěr:
Příklad 4
Najděte globální extrémy funkce \(f: y = {\rm tg}\:x-2x\) na intervalu \((-\dfrac{\pi}{2},\dfrac{\pi}{2})\).
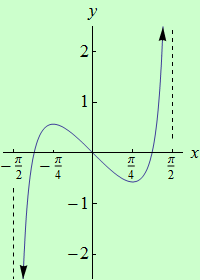 graf funkce |
Všimněte si, že příslušné jednostranné limity v krajních bodech daného intervalu jsou \(-\infty\) a \(+\infty\). Za této situace nemůže existovat ani globální maximum ani globální minimum. Tím je příklad vyřešen.